Luyện tập: giải bài 5 6 7 8 9 trang 69 70 sgk toán 9 tập 1
Luyện tập Bài §1. Góc ở tâm. Số đo cung, Chương III – Góc với đường tròn, sách giáo khoa toán 9 tập hai. Nội dung bài giải bài 4 5 6 7 8 9 trang 69 70 sgk toán 9 tập 2 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 9.
Lý thuyết
1. Góc ở tâm
Góc có đỉnh trùng với tâm của đường tròn được gọi là góc ở tâm.
Cung nằm bên trong góc gọi là cung bị chắn, góc AOB chắn cung nhỏ \(\stackrel\frown{AmB}\) .
Trong trường hợp hình số 2, góc bẹt COD chắn nửa đường tròn.
2. Số đo cung
Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
Số đo của cung lớn bằng hiệu giữa 3600 và số đo của cung nhỏ (có chung 2 mút với cung lớn).
Số đo của nửa đường tròn bằng 1800.
Kí hiệu: số đo cung AB là sđ\(\stackrel\frown{AB}\).
Chú ý:
– Cung nhỏ có số đo nhỏ hơn 1800.
– Cung lớn có số đo lớn hơn 1800.
– Khi hai mút của cung trùng nhau, ta có “cung không” với số đo 00 và cung cả đường tròn có số đo 3600.
3. So sánh hai cung
Trong cùng một đường tròn hay hai đường tròn bằng nhau:
– Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau.
– Trong hai cung, cung nào có số đo lớn hơn được gọi là cung lớn hơn.
4. Khi nào thì sđ\(\stackrel\frown{AB}\) = sđ\(\stackrel\frown{AC}\) + sđ\(\stackrel\frown{CB}\)?
Định lí: Nếu C là một điểm trên cung AB thì: sđ\(\stackrel\frown{AB}\) = sđ\(\stackrel\frown{AC}\) + sđ\(\stackrel\frown{CB}\)
Dưới đây là Hướng dẫn giải bài 4 5 6 7 8 9 trang 69 70 sgk toán 9 tập 2. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Luyện tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần hình học 9 kèm bài giải chi tiết bài 4 5 6 7 8 9 trang 69 70 sgk toán 9 tập 2 của Bài §1. Góc ở tâm. Số đo cung trong Chương III – Góc với đường tròn cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
1. Giải bài 4 trang 69 sgk Toán 9 tập 2
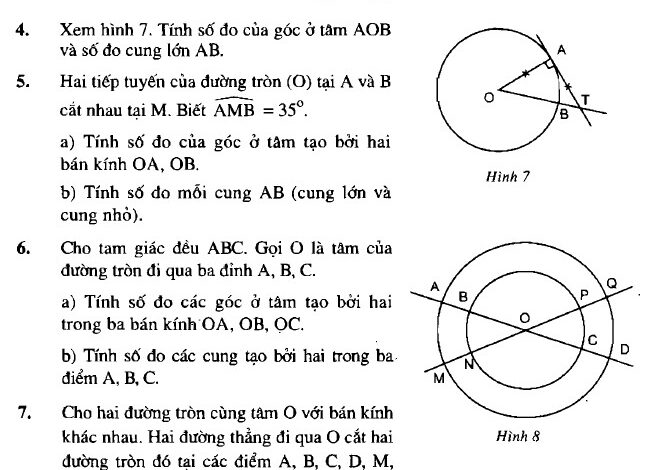
Xem hình 7. Tính số đo góc ở tâm \(AOB\) và số đo cung lớn \(AB\)
Bài giải:
Ta có \(OA = AT\) (gt) nên \(∆AOT\) là tam giác vuông cân tại \(A\), vậy \(\widehat{AOB}=45^0\).
Suy ra số đo cung nhỏ \(\overparen{AB} = 45^0\). Do đó số đo cung lớn \(\overparen{AB}\) là: \(360^0-45^0=315^0\)
2. Giải bài 5 trang 69 sgk Toán 9 tập 2
Hai tiếp tuyến của đường tròn \((O)\) tại \(A\) và \(B\) cắt nhau tại \(M\). Biết \(\widehat{AMB}\).
a) Tính số đo của góc ở tâm tạo bởi hai bán kính \(OA, OB\).
b) Tính số đo mỗi cung \(AB\) (cung lớn và cug nhỏ).
Bài giải:
a) Vì \(MA,MB\) là hai tiếp tuyến của \(\left( O \right)\) cắt nhau tại \(M\) nên \(\widehat {OAM} = 90^\circ ;\,\widehat {MBO} = 90^\circ \)
Xét tứ giác \(OBMA\) có \(\widehat {OAB} + \widehat {OBA} + \widehat {AMB} + \widehat {AOB} = 360^\circ \) (định lý)
Hay \(90^\circ + 90^\circ + 35^\circ + \widehat {AOB} = 360^\circ \\ \Rightarrow \widehat {AOB} = 145^\circ .\)
b) Từ \(\widehat {AOB} = {145^0}\). Suy ra số đo cung nhỏ \(\overparen{AB}\) là \(145^0\) và số đo cung lớn \(\overparen{AB}\) : \({360^0} – {145^0} = {215^0}\)
3. Giải bài 6 trang 69 sgk Toán 9 tập 2
Cho tam giác đều \(ABC\). Gọi \(O\) là tâm của đường tròn đi qua ba đỉnh \(A, B, C\).
a) Tính số đo các góc ở tâm tạo bởi hai trong ba bán kính \(OA, OB, OC\).
b) Tính số đo các cung tạo bởi hai trong ba điểm \(A, B, C\).
Bài giải:
a) Ta có: \(\widehat A = \widehat B = \widehat C = {60^0}\) (gt)
Tâm \(O\) của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của ba cạnh cũng chính là giao điểm của ba đường phân giác của tam giác đều \(ABC\).
Nên \(\widehat {{A_1}} = \widehat {{A_2}} = \widehat {{B_1}} = \widehat {{B_2}} = \widehat {{C_1}} = \widehat {{C_2}} = {30^0}\)
Suy ra: \(\widehat {AOB} = {180^0} – \widehat {{A_1}} – \widehat {{B_1}} = {180^0} – {30^0} – {30^0} = {120^0}\)
Tương tự ta suy ra: \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = {120^0}\)
b) Từ \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = {120^0}\) ta suy ra:
\(sđ\overparen{AB}=sđ\overparen{CA}=sđ\overparen{CB}\) \(= 120^0\)
\(sđ\overparen{ABC}=sđ\overparen{BCA}=sđ\overparen{CAB}\) \(=360^0- 240^0=120^0\)
4. Giải bài 7 trang 69 sgk Toán 9 tập 2
Cho hai đường tròn cùng tâm \(O\) với bán kính khác nhau. Hai đường thẳng đi qua \(O\) cắt hai đường tròn đó tại các điểm \(A, B, C, D, M, N, P, Q\) (h.8)
a) Em có nhận xét gì về số đo của các cung \(AM, CP, BN, DQ\).
b) Hãy nêu tên các cung nhỏ bằng nhau.
c) Hãy nêu tên hai cung lớn bằng nhau.
Bài giải:
a) Các cung nhỏ \(\overparen{AM}, \overparen{CP}, \overparen{BN}, \overparen{DQ}\) có cùng số đo
b) Các cung nhỏ bằng nhau là:
\(\overparen{AM}\) = \(\overparen{DQ}\); \(\overparen{BN}\) = \(\overparen{PC}\); \(\overparen{AQ}\) =\(\overparen{ MD}\); \(\overparen{BP}\) =\(\overparen{NC}\).
c) Các cung lớn bằng nhau:
\(\overparen{AMDQ} = \overparen{MAQD}\); \(\overparen{BNCP} = \overparen{NBPC}\);
5. Giải bài 8 trang 70 sgk Toán 9 tập 2
Mỗi khằng định sau đây đúng hay sai? Vì sao?
a) Hai cung bằng nhau thì có số đo bằng nhau.
b) Hai cung có số đo bằng nhau thì bằng nhau.
c) Trong hai cung, cung nào có số đo lớn hơn là cung lớn hơn.
d) Trong hai cung trên một đường tròn, cung nào có số đo nhỏ hơn thì nhỏ hơn.
Bài giải:
a) Đúng
b) Sai. Không rõ hai cung nằm trên một đường tròn hay trên hai đường tròn bằng nhau không.
c) Sai. Không rõ hai cung nằm trên một đường tròn hay trên hai đường tròn bằng nhau không.
d) Đúng
6. Giải bài 9 trang 70 sgk Toán 9 tập 2
Trên đường tròn tâm \(O\) lấy ba điểm \(A, B, C\) sao cho \(\widehat{AOB} = 100^0\), sđ cung \(\overparen{AC} = 45^0\). Tính số đo của cung nhỏ \(\overparen{BC}\) và cung lớn \(\overparen{BC}\). (Xét cả hai trường hợp: điểm \(C\) nằm trên cung nhỏ \(\overparen{AB}\), điểm \(C\) nằm trên cung lớn \(\overparen{AB}\)).
Bài giải:
♦ TH1: Điểm \(C\) nằm trên cung nhỏ \(\overparen{AB}\)
Số đo cung nhỏ BC là \(sđ \overparen{BC} = sđ \overparen{AB}-sđ \overparen{AC}= 100^0 – 45^0 = 55^0\)
Số đo cung lớn \(\overparen{BC} = 360^0 – 55^0 = 305^0\)
♦ TH2: Điểm \(C\) nằm trên cung lớn \(\overparen{AB}\)
Số đo cung nhỏ BC là \(sđ \overparen{BC} = sđ \overparen{AB}+sđ \overparen{AC}= 100^0 + 45^0= 145^0\)
Số đo cung lớn \(\overparen{BC} = 360^0 – 145^0 = 215^0\)
Bài trước:
Bài tiếp theo:
Xem thêm:
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 9 với giải bài 4 5 6 7 8 9 trang 69 70 sgk toán 9 tập 2!
“Bài tập nào khó đã có giaibaisgk.com“
Giải bài 5 trang 69 sgk toán 9 tập 1
Giải bài 5 trang 69 sách giáo khoa toán 9 tập 1 với lời giải chi tiết, ngắn gọn nhất sẽ giúp các em nắm bắt các kiến thức cơ bản và nâng cao một cách nhanh nhất
Xem chi tiết lời giải tại đây: https://loigiaihay.com/bai5trang69sgktoan9tap1c44a2807.html
Trong tam giác vuông với các cạnh góc vuông có độ dài là 3 và 4 , kẻ đường cao ứng với cạnh huyền. Hãy tính đường cao này và độ dài các đoạn thẳng mà nó định ra trên cạnh huyền.




