Giải bài tập 9: trang 70 sgk hình học lớp 9
Luyện tập Bài §1. Một số hệ thức về cạnh và đường cao trong tam giác vuông, chương I – Hệ thức lượng trong tam giác vuông, sách giáo khoa toán 9 tập một. Nội dung bài giải bài 5 6 7 8 9 trang 69 70 sgk toán 9 tập 1 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 9.
Lý thuyết
1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền
ĐỊNH LÝ 1: Trong một tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
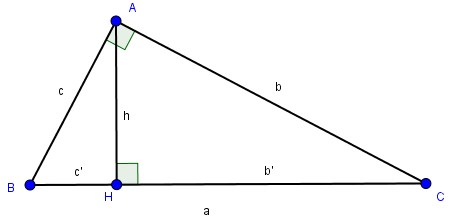
Tam giác ABC vuông tại A, ta có:
\(b^2=a.b’\) , \(c^2=a.c’\)
2. Một số hệ thức liên quan tới đường cao
ĐỊNH LÝ 2: Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
\(h^2=b’.c’\)
ĐỊNH LÝ 3: Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng.
\(b.c=a.h\)
ĐỊNH LÝ 4: Trong một tam giác vuông, nghịch đảo của bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông.
\(\frac{1}{h^2}=\frac{1}{b^2}+\frac{1}{c^2}\) hay \(h=\frac{b.c}{\sqrt{b^2+c^2}}\)
Dưới đây là Hướng dẫn giải bài 5 6 7 8 9 trang 69 70 sgk toán 9 tập 1. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Luyện tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần hình học 9 kèm bài giải chi tiết bài 5 6 7 8 9 trang 69 70 sgk toán 9 tập 1 của bài §1. Một số hệ thức về cạnh và đường cao trong tam giác vuông trong chương I – Hệ thức lượng trong tam giác vuông cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
1. Giải bài 5 trang 69 sgk Toán 9 tập 1
Trong tam giác vuông với các cạnh góc vuông có độ dài là 3 và 4, kẻ đường cao ứng với cạnh huyền. Hãy tính đường cao này và độ dài các đoạn thẳng mà nó định ra trên cạnh huyền.
Bài giải:
Theo định lí Pi-ta-go, ta có:
$BC^2 = AB^2 + AC^2$
$ = 3^2 + 4^2 = 9 + 16 = 25$
$⇒ BC = 5$
Theo định lí 4 về cạnh và đường cao trong tam giác vuông ABC, ta có:
$\frac{1}{AH^2}$ = $\frac{1}{AB^2}$ + $\frac{1}{AC^2}$
= $\frac{1}{9}$ + $\frac{1}{16}$ = $\frac{25}{144}$
⇒ $AH^2$ = $\frac{144}{25}$
$⇒ AH = \frac{12}{5} = 2,5$
Theo định lí 1 về cạnh góc vuông và hình chiếu của nó lên cạnh huyền, ta có:
$AB^2 = BC.BH$
$ ⇒ BH = \frac{AB^2}{BC} = \frac{9}{5} = 1,8$
$⇒ CH = BC – BH = 5 – 1,8 = 3,2$
2. Giải bài 6 trang 69 sgk Toán 9 tập 1
Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 1 và 2. Hãy tính các cạnh góc vuông của tam giác này.
Bài giải:
Ta có $BC = BH + CH = 1 + 2 = 3$
Áp dụng định lí 1 trong tam giác vuông ABC, ta có:
$AB^2 = BC. BH = 3.1 = 3 ⇒ AB = \sqrt{3}$
$AC^2 = BC. CH = 3.2 = 6 ⇒ AC = \sqrt{6}$
3. Giải bài 7 trang 69 sgk Toán 9 tập 1
Người ta đưa ra hai cách vẽ đoạn trung bình nhân x của hai đoạn thẳng a, b (tức là $x^2$ = ab) như trong hai hình sau:
Dựa vào các hệ thức (1) và (2), hãy chứng minh các cách vẽ trên là đúng.
Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.
Bài giải:
Kí hiệu các điểm như hình vẽ trên, ta có:
$OA = OB = OC = \frac{1}{2} BC$ (bằng bán kính đường tròn tâm O)
Tam giác $ABC$ có trung tuyến AO bằng một nửa cạnh tương ứng BC nên $ABC$ là tam giác vuông tại A, kẻ đường cao AH
– Cách 1: Áp dụng hệ thức 2, ta có:
$AH^2 = BH.HC ⇔ x^2 = ab$
– Cách 2: Áp dụng hệ thức 1, ta có:
$AB^2 = BH.BC ⇔ x^2 = ab$
Như vậy các cách vẽ trên đều đúng.
4. Giải bài 8 trang 70 sgk Toán 9 tập 1
Tìm x và y trong mỗi hình sau:
Bài giải:
a) Hình 10: Áp dụng hệ thức 2, ta có:
$x^2 = 4.9 = 36 ⇒ x = 6$
b) Hình 11:
Áp dụng hệ thức 2, ta có:
$2^2 = x.x = 4 ⇒ x = 2$
Áp dụng hệ thức 1, ta có:
$y^2 = x.(x + x) = 2.(2 + 2) = 8$
$⇒ y = 2\sqrt{2}$
c) Hình 12:
Áp dụng hệ thức 2, ta có:
$12^2 = x.16 ⇒ x = \frac{144}{16} = 9$
Áp dụng hệ thức 1, ta có:
$y^2 = x.(x + 16) = 9.(9 + 16) = 225$
$ ⇒ y = 15$
5. Giải bài 9 trang 70 sgk toán 9 tập 1
Cho hình vuông $ABCD$. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ơ K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:
a) Tam giác $DIL$ là một tam giác cân.
b) Tổng $\frac{1}{DI^2} + \frac{1}{DK^2}$ không đổi khi I thay đổi trên cạnh $AB$.
Bài giải:
a) Hai tam giác vuông $DAI$ và $DCL$ có:
$AD = DC$
$\widehat{D_1}$ = $\widehat{D_2}$ (Vì cùng phụ với $\widehat{D_3}$)
Nên $\Delta$DAI = $\Delta$DCL
Suy ra $DI = DL$
Do đó $\Delta DIL$ cân tại $D$.
b) Trong tam giác vuông $\Delta DKL$ có $DC$ là đường cao ứng với cạnh huyền nên theo hệ thức 4, ta có:
$\frac{1}{DC^2} = \frac{1}{DL^2} + \frac{1}{DK^2}$
Hay $\frac{1}{DC^2} = \frac{1}{DI^2} + \frac{1}{DK^2}$
Mặt khác $DC$ là cạnh của hình vuông $ABCD$ nên $DC$ không đổi, điều đó cũng có nghĩa là $\frac{1}{DC^2}$ không đổi.
Do đó $\frac{1}{DI^2} + \frac{1}{DK^2}$ không đổi.
Bài trước:
Bài tiếp theo:
Xem thêm:
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 9 với giải bài 5 6 7 8 9 trang 69 70 sgk toán 9 tập 1!
“Bài tập nào khó đã có giaibaisgk.com“
Giải bài 9 trang 70 SGK toán 9 tập 1
Giải bài 9 trang 70 sách giáo khoa toán 9 tập 1 với lời giải chi tiết, ngắn gọn nhất sẽ giúp các em nắm bắt các kiến thức cơ bản và nâng cao một cách nhanh nhất
Xem chi tiết lời giải tại đây: https://loigiaihay.com/bai9trang70sgktoan9tap1c44a2812.html
Cho hình vuông ABCD . Gọi I là một điểm nằm giữa A và B . Tia DI và tia CB cắt nhau ở K . Kẻ đường thẳng qua D , vuông góc với DI . Đường thẳng này cắt đường thẳng BC tại L . Chứng minh rằng
a) Tam giác DIL là một tam giác cân;
b) Tổng \\dfrac{1}{DI^{2}}+\\dfrac{1}{DK^{2}} không đổi khi I thay đổi trên cạnh AB .




