Dấu của nhị thức bậc nhất: định lý, cách lập bảng xét dấu và bài tập

Bạn đang xem: Dấu của nhị thức bậc nhất: định lý, cách lập bảng xét dấu và bài tập Tại Website vuongquocdongu.com

Định nghĩa nhị thức là gì?

Trong đại số, nhị thức được định nghĩa là một đa thức với hai số hạng – tổng của hai đơn thức. Đây cũng chính là dạng đa thức đơn giản nhất sau đơn thức.

Nhắc lại về nhị thức bậc nhất

• Nhị thức bậc nhất (đối với x) là biểu thức dạng \(ax+b\)

  , trong đó a và b là hai số cho trước với \(a \neq0\)

• \(x_0= \frac{-b}{a}\) được gọi là nghiệm của nhị thức bậc nhất \(f(x) =ax+b\)

Định lý dấu của nhị thức bậc nhất

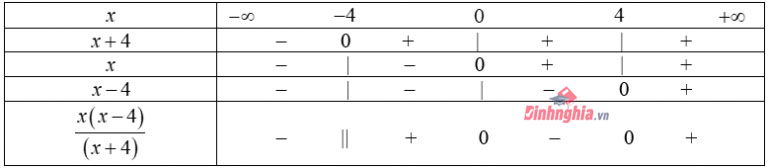
Trong toán học, nhị thức \(f(x) =ax+b(a\neq0)\) cùng dấu với hệ số a khi x lấy giá trị trong khoảng \(\left (\frac{-b}{a};+\infty \right )\) và trái dấu với hệ số a khi x lấy giá trị trong khoảng \(\left (-\infty ;\frac{-b}{a} \right )\). Nội dung định lý được mô tả trong bảng xét dấu của \(f(x)=ax+b\).

Minh họa bằng đồ thị:

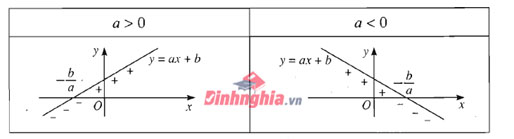
Giả sử f(x) là một tích của những nhị thức bậc nhất. Áp dụng định lý về dấu của nhị thức bậc nhất có thể xét dấu từng nhân tử. Lập bảng xét dấu chung cho tất cả các nhị thức bậc nhất có mặt trong f(x) ta suy ra được dấu của f(x). Trường hợp f(x) là một thương cũng được xét tương tự.

Giải bất phương trình \(f(x) > 0\) thực chất là xét xem biểu thức \(f(x)\) nhận giá trị dương với những giá trị nào của x (do đó cũng biết \(f(x)\) nhận giá trị âm với những giá trị nào của x), làm như vậy ta nói đã xét dấu biểu thức \(f(x)\)

Giải bất phương trình tích

Các dạng toán thường gặp: \(P(x)>0,P(x)\geq 0,P(x)<0,P(x)\leq0\) trong đó P(x) là tích các nhị thức bậc nhất.

Lập bảng xét dấu của P(x), từ đó suy ra tập nghiệm của bất phương trình.

Ví dụ: Giải bất phương trình: \((x-2)(x+1)(3x-4)>0\)

1. \((x-2)(x+1)(3x-4)>0\hspace{1.5cm}(1)\) 

• Đặt \(P(x)=(x-2)(x+1)(3x-4)\) 

• Giải phương trình \(P(x)=0\) ta được: \(x=2;x=-1;x=\frac {4}{3}\)

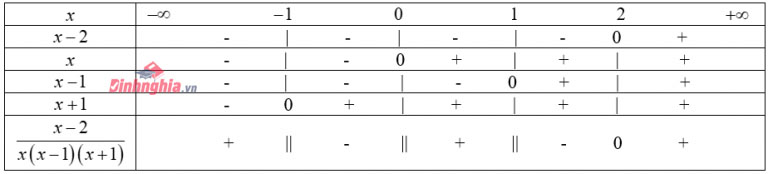
• Sắp xếp các giá trị tìm được của x theo giá trị tăng: \(-1,\frac{4}{3},2\). Ba số này chia thành bốn khoảng. Ta xác định dấu của \(P(x)\) trên từng khoảng bằng cách lập bảng xét dấu của \(P(x)\)

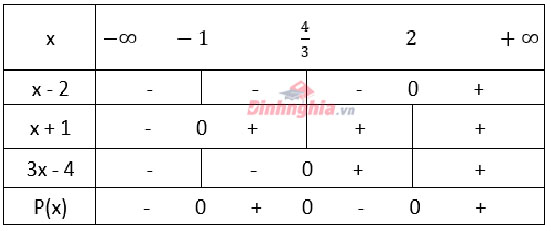
Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình (1) là:\(\left ( -1;\frac{4}{3} \right )\cup\left(2;+\infty \right)\)

Giải bất phương trình chứa ẩn ở mẫu 

Các dạng toán thường gặp: \(\frac{P(x)}{Q(x)} > 0, \frac{P(x)}{Q(x)} \geq 0, \frac{P(x)}{Q(x)} < 0, \frac{P(x)}{Q(x)}\leq0\), trong đó P(x) và Q(x) là tích những nhị thức bậc nhất.

Lập bảng xét dấu của \(\frac{P(x)}{Q(x)}\), từ đó suy ra tập nghiệm của bất phương trình.

Ví dụ: Giải bất phương trình:\(\frac{4}{x-3} \leq\frac{6}{3x+2}\hspace{1.5cm} (1)\)

Ta có: 

\((1)\Leftrightarrow\frac{4}{x-3}-\frac{6}{3x+2}\leq0\\ \Leftrightarrow \frac{4(3x+2)-6(x-3)}{(x-3)(3x+2)}\leq0\\ \Leftrightarrow\frac{6x+26}{(x-3)(3x+2)}\leq0\)

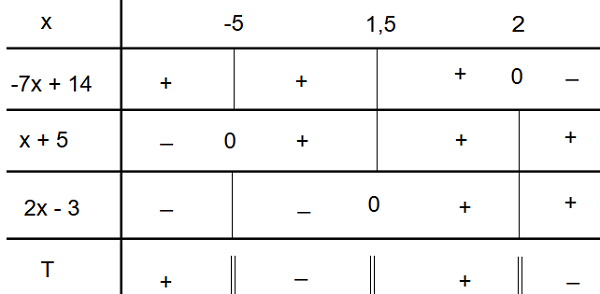
Ta lập bảng xét dấu của bất phương trình (2): 

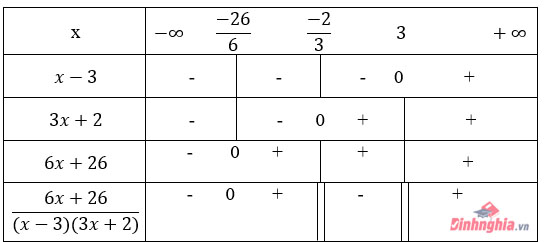
Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình (2) là: \(\left (-\infty;\frac{-26}{6} \right ]\cup\left (\frac{-2}{3};3\right )\)

Giải bất phương trình chứa ẩn trong dấu giá trị tuyệt đối

Sử dụng định nghĩa hoặc tính chất của giá trị tuyệt đối để khử dấu giá trị tuyệt đối. Ta thường phải xét phương trình hay bất phương trình trong nhiều khoảng (đoạn, nửa đoạn) khác nhau, trên đó mỗi biểu thức nằm trong dấu giá trị tuyệt đối đều có một dấu xác định.

Ví dụ: Giải bất phương trình: \(|2x-1| < 3x+5\hspace{1.5cm}(3)\)

• Với \(x < \frac{1}{2}\), ta có: 

\((3)\Leftrightarrow1-2x<3x+5\Leftrightarrow5x>-4\Leftrightarrow x>-\frac{4}{5}\)

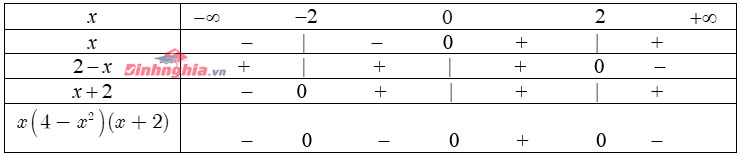
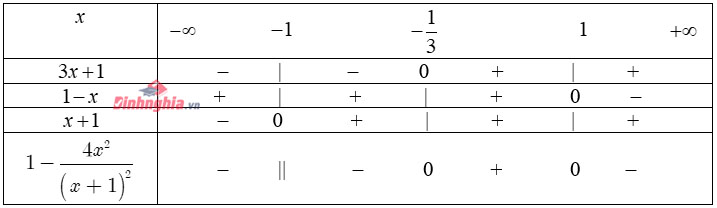
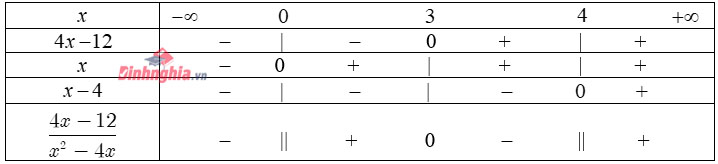
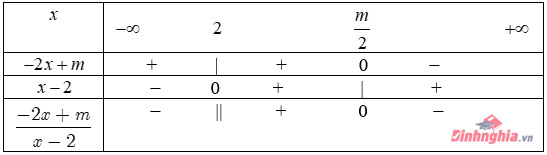
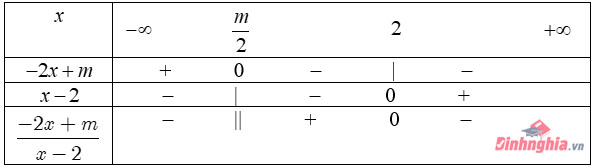
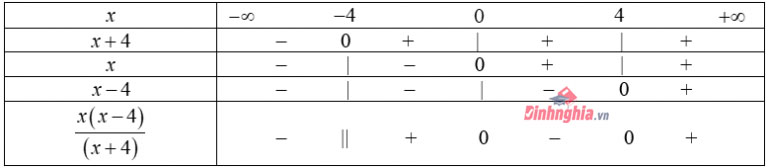
Kết hợp với điều kiện \(x<\frac{1}{2}\), ta được \(-\frac{4}{5}

• Với \(x\geq\frac{1}{2}\), ta có: 

\((3)\Leftrightarrow 2x-1<3x+5\Leftrightarrow x>-6\)

Kết hợp với điều kiện \(x\geq\frac{1}{2}\), ta được \(x\geq\frac{1}{2}\).

Kết luận: Tập nghiệm của bất phương trình (3) : \(\left (-\frac{4}{5};\frac{1}{2} \right )\cup\left [\frac{1}{2};+\infty \right )=\left ( -\frac{4}{5};+\infty \right )\)

Các dạng toán về dấu của nhị thức bậc nhất

Lập bảng xét dấu biểu thức chứa nhị thức bậc nhất

Ví dụ 1: 

1. \(x(4-x^2)(x+2)\)

2. \(1-\frac{4x^2}{(x+1)^2}\)

3. \(\frac{4x-12}{x^2-4x}\)

Cách giải: 

1. Ta có: \(x(4-x^2)(x+2)=x(2-x)(x+2)^2\)

Bảng xét dấu: 

    2. Ta có: \(1-\frac{4x^2}{(x+1)^2}=\frac{(x+1)^2-4x^2}{(x+1)^2}= \frac{(3x+1)(1-x)}{(x+1)^2}\)

Bảng xét dấu: 

   3. Ta có: \(\frac{4x-12}{x^2-4x}=\frac{4x-12}{x(x-4)}\)

Bảng xét dấu: 

Ví dụ 2: Tùy vào \(m\) xét dấu biểu thức sau \(\frac{-2x+m}{x-2}\)

Cách giải: 

Ta có: \(x-2=0\Leftrightarrow x=2\\ -2x+m=0\Leftrightarrow x=\frac{m}{2}\)

Trường hợp 1: \(\frac{m}{2}>2\Leftrightarrow m>4\)

Bảng xét dấu: 

Suy ra \(\frac{-2x+m}{x-2}>0\Leftrightarrow x\in\left ( 2;\frac{m}{2} \right )\) và \(\frac{-2x+m}{x-2}<0\Leftrightarrow x\in\left ( -\infty;2 \right )\cup\left ( \frac{m}{2};+\infty \right )\)

Trường hợp 2: \(\frac{m}{2}=2\Leftrightarrow m=4\)

Ta có \(\frac{-2x+m}{x-2}=\frac{-2x+2}{x-2}=-2\)

Suy ra \(\frac{-2x+m}{x-2}<0\Leftrightarrow x\in\mathbb{R}\setminus \left \{ 2 \right \}\)

Trường hợp 3: \(\frac{m}{2}<2\Leftrightarrow m<4\)

Bảng xét dấu: 

Suy ra \(\frac{-2x+m}{x-2}>0\Leftrightarrow x\in\left ( \frac{m}{2};2 \right )\) và \(\frac{-2x+m}{x-2}<0\Leftrightarrow x\in\left (-\infty; \frac{m}{2} \right )\cup\left ( 2;+\infty \right )\).

Tìm hiểu ứng dụng xét dấu của nhị thức bậc nhất

Ví dụ 1: Giải các bất phương trình sau: 

1. \(x(\sqrt{3}x-3)(3-x^2)\leq0\)

2. \(\frac{1}{(x-2)^2}\leq\frac{1}{x+4}\)

3. \(||2x-1|-4|>3\)

4. \(|x+1|-|x-2|\geq3\)

5. \(\frac{|x-1|-1}{x^4-x^2}\)

1. Ta có: \(x(\sqrt{3}x-3)(3-x^2)\leq0\Leftrightarrow x\sqrt{3}(x-\sqrt3)(\sqrt3-x)(\sqrt3+x)\leq0\Leftrightarrow -\sqrt3x(x-\sqrt3)^2(x+\sqrt3)\leq0\)

\(\Leftrightarrow\left[ \begin{array}{ll} x=\sqrt3 & \\ x(x+\sqrt3)\ge0 & \end{array} \right.\)

Bảng xét dấu: 

Suy ra \(x(x+\sqrt3)\ge0\Leftrightarrow x\in \left ( -\infty;-\sqrt3 \right ]\cup \left [0;+\infty \right )\).

Vậy tập nghiệm của phương trình là: \(S=\left ( -\infty;-\sqrt3 \right ]\cup \left [0;+\infty \right )\)

    2. Điều kiện xác định: \(\left\{\begin{matrix} x\ne2 & \\ x\ne -4 & \end{matrix}\right.\)

Ta có:

\(\frac{1}{(x-2)^2}\leq\frac{1}{x+4} \Leftrightarrow \frac{1}{x+4}-\frac{1}{(x-2)^2}\ge0\\ \Leftrightarrow\frac{x^2-4x}{(x+4)(x-2)^2}\ge0\Leftrightarrow\frac{x(x-4)}{(x+4)(x-2)^2}\ge0\\ \Leftrightarrow\frac{x(x-4)}{(x+4)}\). Do \((x-2)^2\) luôn dương nên ta chỉ xét các phần tử còn lại.

Kết hợp với điều kiện xác định ban đầu, suy ra tập nghiệm của bất phương trình là: \(S=\left (-4;0 \right ]\cup\left [4;+\infty \right )\).

   3. Ta có: 

\(||2x-1|-4|>3\Leftrightarrow\left[ \begin{array}{ll} |2x-1|-4>3 & \\ |2x-1|-4<-3 & \end{array} \right.\\ \Leftrightarrow\left[ \begin{array}{ll} |2x-1|>7 & \\ |2x-1|<1 & \end{array} \right.\Leftrightarrow\left[ \begin{array}{ll} 2x-1>7 & \\ 2x-1<-7 & \\-1<2x-1<1 \end{array} \right.\\ \Leftrightarrow\left[ \begin{array}{ll} x>4 & \\ x<-3 & \\0

Vậy tập nghiệm của bất phương trình là: \(S=\left ( -\infty;-3 \right )\cup\left ( 0;1 \right )\cup\left ( 4;+\infty \right )\)

    4. Bảng xét dấu: 

Từ bảng xét dấu đó ta chia ra các trường hợp sau: 

• Với \(x<-1\) ta có bất phương trình tương đương với \(-(x+1)+(x-2)\ge3\Leftrightarrow-3\ge3\) (vô nghiệm).

• Với \(-1\le x\le2\) ta có bất phương trình tương đương với \((x+1)+(x-2)\ge3\Leftrightarrow x\ge2\). Kết hợp với điều kiện \(-1\le x\le2\) suy ra bất phương trình vô nghiệm.

• Với \(x\ge2\) ta có bất phương trình tương đương với \((x+1)-(x-2)\ge3\Leftrightarrow 3\ge3\). Kết hợp với điều kiện \(x\ge2\) suy ra bất phương trình có nghiệm là \(x\ge2\)

Vậy tập nghiệm của bất phương trình là \(S=\left [2;+\infty \right )\)

   5. Điều kiện xác định: \(x^4-x^2\ne0\Leftrightarrow\left\{\begin{matrix} x\ne0 & \\ x\ne\pm 1 & \end{matrix}\right.\)

Ta có: 

\(\frac{|x-1|-1}{x^4-x^2}\ge0\Leftrightarrow\frac{(|x-1|+1)(|x-1|-1)}{x^4-x^2}\ge0\Leftrightarrow\frac{|x-1|^2-1}{x^4-x^2}\\ \Leftrightarrow\frac{x^2-2x}{x^4-x^2}\ge0\Leftrightarrow\frac{x(x-2)}{x^2(x-1)(x+1)}\ge0\Leftrightarrow\frac{x-2}{x(x-1)(x+1)}\ge0\)

Bảng xét dấu: 

Vậy tập nghiệm của bất phương trình là: \(S=\left ( -\infty;-1 \right )\cup\left ( 0;1 \right )\cup\left [2;+\infty \right )\).

Ví dụ 2:

Xem chi tiết qua tài liệu cùng bài giảng dưới đây:

(Nguồn: www.youtube.com)

dau-cua-nhi-thuc-bac-nhat-7

Xem thêm:

Rate this post

Please follow and like us:

Xem thêm bài viết thuộc chuyên mục: Giáo Dục