Giải hệ phương trình

Bạn đang xem: Giải hệ phương trình Tại Website vuongquocdongu.com

Hệ phương trình đối xứng là gì?

Hệ phương trình đối xứng là hệ phương trình mà khi ta thay đổi vai trò của (x, y ) cho nhau thì hệ phương trình không thay đổi. Trong đó ta chia thành hai dạng hệ phương trình đối xứng cơ bản là loại 1 và loại 2.

Làm thế nào để phân loại một hệ phương trình đối xứng?

Là hệ phương trình mà khi ta đổi vai (x; y ) thì mỗi phương trình không đổi hay nói cách khác là hệ phương trình đối xứng loại 1 (HPTDXL1) là hệ phương trình trong đó có hai ẩn số (x; y ) đối xứng trong mỗi phương trình

( left { begin {matrix} f (x; y) = 0 \ g (x; y) = 0 end {matrix} right. ) trong đó: ( left { begin {matrix} f (x; y) = f (y; x) \ g (x; y) = g (y; x) end {matrix} right. )

Hệ phương trình đối xứng loại một với hai ẩn số

Là hệ phương trình mà khi ta đổi vai (x; y ) thì phương trình này trở thành phương trình khác và ngược lại hay nói cách khác là hệ phương trình đối xứng loại 2 (HPTDXL2) là hệ phương trình gồm 2 phương trình. đối xứng

( left { begin {matrix} f (x; y) = 0 \ f (y; x) = 0 end {matrix} right. )

Hệ phương trình đối xứng loại 2 ẩn số

giải hệ phương trình đối xứng loại 2″ class=”wp-image-10879″ height=”344″ src=”https://vuongquocdongu.com/wp-content/uploads/2021/12/1636000360_339_Cac-phuong-phap-giai-He-phuong-trinh-doi-xung-loai.png” title=”cách giải hệ phương trình đối xứng loại 2″ width=”468″/>

Cách nhận biết hệ phương trình đối xứng

Để xác định một hệ phương trình đối xứng loại 1, ta xét từng phương trình, thử thay đổi (x rightarrow y; y rightarrow x ) xem phương trình mới thu được có giống với phương trình ban đầu hay không.

Hệ thống ( left { begin {matrix} x ^ 2 + 2x + 2y + y ^ 2-1 = 0 \ x ^ 3 + y ^ 3 + xy = 1 end {matrix} right. ) là một hệ phương trình đối xứng loại một.

Hệ thống ( left { begin {matrix} x ^ 3-y ^ 3 + xy = 1 \ x ^ 2 + 2xy + x + y + y ^ 2 = 3 end {matrix} right. ) không phải là một hệ phương trình đối xứng loại một.

Để xác định hệ phương trình đối xứng loại 1, ta xét phương trình thứ nhất, thử biến đổi (x rightarrow y; y rightarrow x ) xem phương trình mới thu được có giống phương trình thứ hai không? Làm tương tự với phương trình thứ hai.

Ví dụ:

Hệ thống ( left { begin {matrix} x ^ 3-x ^ 2y = x \ y ^ 3-xy ^ 2 = y end {matrix} right. ) Là một hệ phương trình đối xứng của loại thứ hai.

Hệ thống ( left { begin {matrix} x ^ 2-xy = y \ y ^ 2 + xy = x end {matrix} right. ) Không phải là một hệ phương trình đối xứng

Phương pháp giải hệ phương trình đối xứng loại 1

Đây là phương pháp chung để giải hệ phương trình đối xứng loại một.

• Bước 1:

  Đặt (S = x + y; P = xy ). Biến đổi mỗi phương trình thành phương trình mới bởi (2 ) ẩn (S; P )

• Bước 2:

  Giải hệ phương trình để tìm (S; P ) thỏa mãn (S ^ 2 geq 4P )

• Bước 3:

  Giải phương trình (

  t ^ 2-St + P ). Khi đó (x; y ) là nghiệm của phương trình trên (theo định lý Viet).

Để chuyển hệ phương trình về dạng (S; P ), chúng ta cần nhớ một số đẳng thức quan trọng:

(x ^ 2 + y ^ 2 = (x + y) ^ 2 -2xy = S ^ 2-2P )

(| xy | = sqrt {(x + y) ^ 2-4xy} = sqrt {S ^ 2-4P} )

(x ^ 3 + y ^ 3 = (x + y) (x ^ 2 + y ^ 2-xy) = S (S ^ 2-3P) )

Nếu ((x; y) = (a; b) ) là nghiệm của hệ phương trình thì ((x; y) = (b; a) ) cũng là nghiệm của hệ phương trình .

Giải hệ phương trình:

( left { begin {ma trận} x + xy + y = 2 \ x ^ 2 + xy + y ^ 2 = 4 end {matrix} right. )

Đặt (S = x + y; P = xy ). Thời hạn: (S ^ 2 geq 4P )

Thay vào hệ phương trình ta được:

( left { begin {matrix} S + P = 2 \ S ^ 2-P = 4 end {matrix} right. )

Thay (-P = S-2 ) vào phương trình dưới đây, ta được:

(S ^ 2 + S-6 = 0 Leftrightarrow (S-2) (S + 3) = 0 )

( Leftrightarrow left[begin{array}{l} S=2 ; P =0\S=-3 ; P=5end{array}right.)

Kiểm tra điều kiện ( S^2 geq 4P ), vậy (left{begin{matrix} S=2\ P=0 end{matrix}right.)

Vậy ( x;y ) là nghiệm của phương trình ( t^2-2t =0 )

(Leftrightarrow left[begin{array}{l}t=0 \t=2 end{array}right.)

Vậy hệ phương trình đã cho có hai cặp nghiệm ( (x;y) = ( 0;2) ; (2;0) )

Đây là phương pháp để giải các bài toán hệ phương trình đối xứng loại 1 khó. Những hệ này nếu nhìn qua thì ta sẽ thấy nó không phải là đối xứng. Nhưng khi chúng ta đặt ẩn phụ một cách thích hợp, bài toán sẽ trở thành hệ phương trình đối xứng loại 1. Từ đó chúng ta có thể giải một cách dễ dàng.

Giải hệ phương trình : (left{begin{matrix} x(x+2)(2x+y)-9=0\ x^2+4x+y=6 end{matrix}right.)

Đặt ( x^2+2x= a ; 2x+y=b ). Thay vào hệ đã cho ta được :

(left{begin{matrix} ab=9 \a+b =6 end{matrix}right.)

Vậy ( a;b ) là nghiệm của phương trình :

( t^2-6t+9= 0 Leftrightarrow (t-3)^2=0 Leftrightarrow t=3 )

Vậy ( a=b=3 )

Thay vào ta được:

(left{begin{matrix} x^2+2x=3\2x+y=3 end{matrix}right. Leftrightarrow left{begin{matrix} (x+3)(x-1)=0\ 2x+y=3 end{matrix}right.)

(Leftrightarrow left[begin{array}{l}left{begin{matrix} x=-3\y=9 end{matrix}right.\ left{begin{matrix} x=1\y=1 end{matrix}right. end{array}right.)

Vậy phương trình đã cho có ( 2 ) cặp nghiệm :

( (x;y) =(-3;9) ; (1;1) )

Với những hệ phương trình này, cách giải vẫn bao gồm các bước như trên nhưng chúng ta cần thêm bước tìm ĐKXĐ của hệ phương trình.

Giải hệ phương trình:

(left{begin{matrix} x+y-sqrt{xy}=3\ sqrt{x+1} + sqrt{y+1}=4 end{matrix}right.)

ĐKXĐ:

(left{begin{matrix} x geq -1\y geq -1 \ xy geq 0 end{matrix}right. hspace{1cm} (*))

Đặt (S=x+y hspace{5mm}; P=xy) với (left{begin{matrix} S^2 geq 4P\ Pgeq 0 \ S geq -2 end{matrix}right. hspace{1cm} (**))

Bình phương 2 vế PT (2) hệ phương trình đã cho tương đương với :

(left{begin{matrix} x+y-sqrt{xy}=3\ x+y+2+sqrt{x+y+xy+1}=16 end{matrix}right.)

(Leftrightarrow left{begin{matrix} S- sqrt{P} =3 \S+2+2sqrt{S+P+1}=16 end{matrix}right.)

(Leftrightarrow left{begin{matrix} P= S^2 -6S +9\ S -14 =-2sqrt{S+P+1} end{matrix}right.) với (3leq Sleq 14)

Thay ( P= S^2 -6S +9 ) từ PT (1) vào PT (2) ta có :

(S-14 = -2sqrt{S^2-5S+10})

(Leftrightarrow S^2-28S+196 = 4(S^2-5S+10))

(Leftrightarrow 3S^2+8S-156=0 Leftrightarrow (S-6)(3S+26)=0)

(Leftrightarrow left{begin{matrix} S=6\S=-frac{26}3{} end{matrix}right.)

Kết hợp ĐKXĐ ta được (S=6 Rightarrow P=9)

Vậy (x;y) là nghiệm của phương trình :

(t^2-6t+9 =0 Leftrightarrow t=3)

Vậy (x=y=3) ( thỏa mãn điều kiện). 

Bài tập hệ phương trình đối xứng loại 1

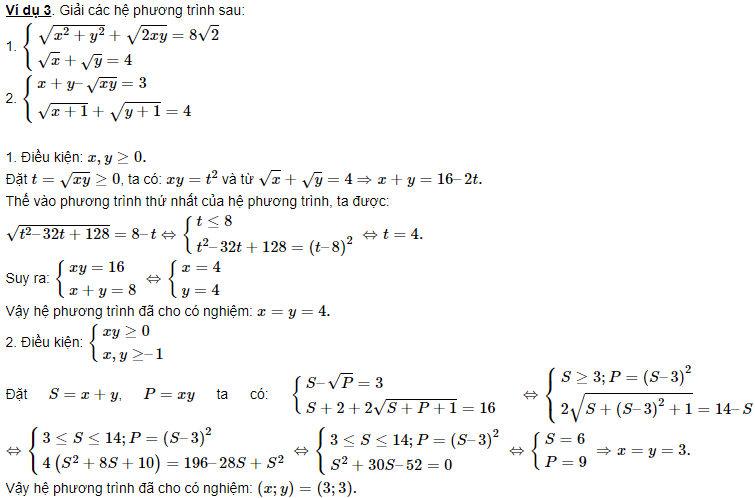
Sau đây là một số bài tập để các bạn luyện tập phần hệ phương trình đối xứng loại 1.

Bài 1: Giải hệ phương trình:

(left{begin{matrix} x^2+xy+y^2=7\x^2+y^2+x+y=8 end{matrix}right.)

Bài 2: Giải hệ phương trình:

(left{begin{matrix} x+y+frac{1}{x}+frac{1}{y}=5\x^2+y^2+frac{1}{x^2}+frac{1}{y^2}=9 end{matrix}right.)

Bài 3: Tìm (m ) để hệ thống có chính xác (2 ) giải pháp:

( left { begin {matrix} (x + y) ^ 2 = 4 \ x ^ 2 + y ^ 2 = 2m + 2 end {matrix} right. )

Phương pháp giải hệ phương trình đối xứng loại 2

Đây là phương pháp chung để giải phương trình đối xứng loại 2.

• Bước 1:

  Trừ các vế tương ứng của hai phương trình, biến phương trình thu được thành phương trình tích: ((xy) .f (x; y) = 0 )

• Bước 2:

  Giải phương trình (f (x; y) = 0 ) để tìm quan hệ (x; y ). Sau đó, thay một phương trình trong hệ ban đầu để giải cho (x; y ) (lưu ý trường hợp của (xy = 0 ))

• Bước 3:

  Kết luận kiểm tra.

Giải hệ phương trình:

( left { begin {matrix} x ^ 3 = 3x + 8y \ y ^ 3 = 3y + 8x end {matrix} right. )

Để giải hệ phương trình đối xứng bậc 2 này, chúng ta cần nhớ hằng đẳng thức: (A ^ 3-B ^ 3 = (AB) (A ^ 2 + AB + B ^ 2) )

Trừ cả hai vế của hai phương trình ta được:

((x ^ 3-y ^ 3) +5 (xy) = 0 Left rightarrow (xy) (x ^ 2 + xy + y ^ 2 + 5) = 0 ; ; ; ; (1) )

Ta có: (x ^ 2 + xy + y ^ 2 + 5 = (x + frac {y} {2}) ^ 2+ frac {3y ^ 2} {4} +5 geq 5> 0 )

Vì vậy, từ ((1) Rightarrow x = y )

Thay vào đó, chúng tôi nhận được:

(x ^ 3 = 11x Leftrightarrow left[begin{array}{l} x=0\x=pm sqrt{11} end{array}right.)

Vậy phương trình đã cho có ( 3 ) cặp nghiệm thỏa mãn : ( (x;y) =(0;0) ; (sqrt{11};sqrt{11}) ; (-sqrt{11};-sqrt{11}) )

Như ta biết thì hệ phương trình ĐX bậc hai là một dạng hệ phương trình đối xứng vòng quanh gồm ( 2 ) ẩn dạng:

(left{begin{matrix} f(x)=g(y)\f(y)=g(x) end{matrix}right.)

Nếu ta chứng minh được hàm số ( f

( f(x) leq f(y) =g(x) leq g(y) )

Mà mặt khác do ( f(x) =g(y) ) nên đẳng thức xảy ra. Vậy ( f(x)=g(x) ). Giải phương trình thu được [/latex] NS [/latex] , từ đó tìm ra nghiệm của hệ phương trình

Trong trường hợp hàm (f

Đây cũng là phương pháp giải các bài toán về phương trình đối xứng xung quanh nhiều ẩn số:

( left { begin {matrix} f (x) = g (y) \ f (y) = g (z) \ f (z) = g (x) end {matrix} right. )

Giải hệ phương trình:

( left { begin {matrix} x ^ 3 + x = 3y \ y ^ 3 + y = 3x end {matrix} right. )

Xét hàm (f

Dễ dàng thấy rằng cả (f

(f (x) leq f (y) = g (x) leq g (y) )

Nhưng vì (f (x) = g (y) ) (theo hệ phương trình) nên đẳng thức xảy ra, vì vậy (f (x) = g (x) )

Do đó: (x ^ 3 + x = 3x Mũi tên trái x (x ^ 2-2) = 0 )

( Leftrightarrow left[begin{array}{l} x=0\x=pm sqrt{2} end{array}right.)

Vậy hệ phương trình có ( 3 ) cặp nghiệm ((x;y)=(0;0);(sqrt{2};sqrt{2});(-sqrt{2};-sqrt{2}))

Đây là một dạng hệ phương trình đối xứng loại 2 khó do có căn thức nên nều trừ trực tiếp như cách thông thường thì sẽ không xuất hiện biểu thứ ( (x-y) ) ngay. Do đó chúng ta cần phải sử dụng phương pháp nhân liên hợp để biến đổi tạo ra nhân tử ( (x-y) ). Một số biến đổi cần lưu ý :

(sqrt{a}-sqrt{b} = frac{a-b}{sqrt{a}+sqrt{b}})

(sqrt[3]{a} – sqrt[3]{b} = frac {ab} { sqrt[3]{a ^ 2} + sqrt[3]{ab} + sqrt[3]{b ^ 2}} )

Ngoài ra còn phải sử dụng cách đặt ẩn phụ là biểu thức chứa căn để tạo ra một hệ mới không chứa căn.

Kiểm tra ĐIỀU KIỆN trước khi giải quyết.

Giải hệ phương trình ( left { begin {matrix} sqrt {x + 5} + sqrt {y-2} = 7 \ sqrt {y + 5} + sqrt {x-2} = 7 end {matrix} right. )

Điều khoản: (x; y geq 2 )

Trừ cả hai vế của hai phương trình ta được: (( sqrt {x + 5} – sqrt {y + 5}) – ( sqrt {x-2} – sqrt {y-2}) = 0 )

( Leftrightarrow (xy) ( frac {1} { sqrt {x + 5} + sqrt {y + 5}} – frac {1} { sqrt {x-2} + sqrt {y- 2}}) = 0 ; ; ; ; ; (1) )

Chúng ta có:

( left { begin {matrix} sqrt {x + 5}> sqrt {x-2} \ sqrt {y + 5}> sqrt {y-2} end {matrix} right Rightarrow sqrt {x + 5} + sqrt {y + 5}> sqrt {x-2} + sqrt {y-2} )

( Rightarrow frac {1} { sqrt {x + 5} + sqrt {y + 5}} < frac {1} { sqrt {x-2} + sqrt {y-2}} )

Vì vậy, ( Rightarrow frac {1} { sqrt {x + 5} + sqrt {y + 5}} – frac {1} { sqrt {x-2} + sqrt {y-2}} <0 )

Do đó từ ((1) Rightarrow x = y )

Thay vào đó, chúng tôi nhận được:

( sqrt {x + 5} + sqrt {x-2} = 7 Mũi tên trái 2x + 3 + 2 sqrt {x ^ 2 + 3x-10} = 49 )

( Mũi tên trái 23-x = sqrt {x ^ 2 + 3x-10} Mũi tên phải x ^ 2-46x + 529 = x ^ 2 + 3x-10 )

( Rightarrow 49x = 539 Rightarrow x = 11 ) (hài lòng)

Vì vậy (x = y = 11 )

Xem chi tiết >>> Phương trình chứa nghiệm nguyên: Lý thuyết, Lời giải và Bài tập

Bài tập về hệ phương trình đối xứng loại 2

Ví dụ 3: Giải hệ phương trình dưới đây.

Vậy hệ phương trình đã cho có nghiệm x = y = 3

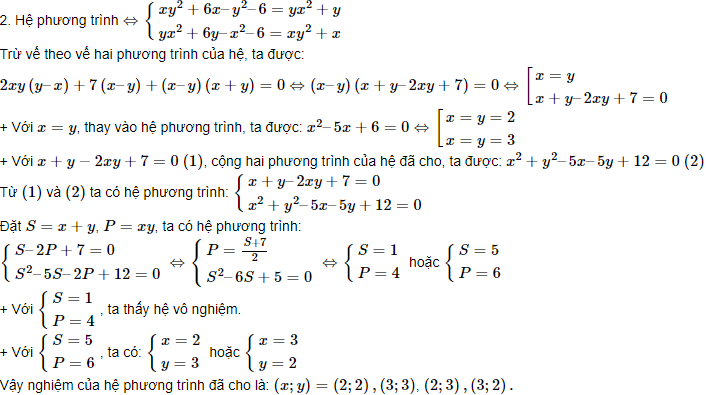
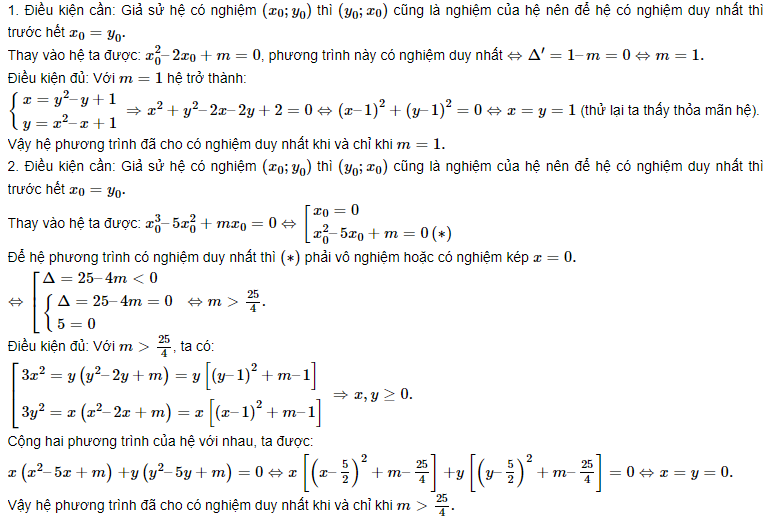
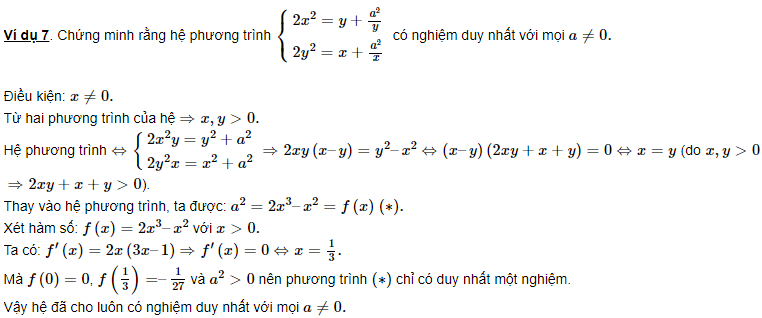
Dưới đây là một số bài tập rèn luyện hệ phương trình đối xứng loại 2.

Bài 1: Giải hệ phương trình:

( left { begin {matrix} 2x + 3 + sqrt {4-y} = 4 \ 2y + 3 + sqrt {4-x} = 4 end {matrix} right. )

Bài 2: Giải hệ phương trình:

( left { begin {matrix} x + sqrt[4]{y-1} = 1 \ y + sqrt[4]{x-1} = 1 end {matrix} right. )

Bài 3:

Tìm (m ) để hệ phương trình sau có nghiệm duy nhất

( left { begin {matrix} x ^ 2-x-y + m = 0 \ y ^ 2-y-x + m = 0 end {matrix} right. )

Phương trình với hệ số đối xứng là gì?

Phương trình có đối xứng bậc (n ) là một phương trình có dạng (f (x) = 0 ) trong câu đố (f (x) ) là một đa thức với tất cả các số hạng được sắp xếp từ bậc cao hơn đến bậc thấp hơn ( (x ^ n; x ^ {n-1};…; x; x ^ 0 )) sao cho mỗi cặp hệ số cách đều cả hai đầu bằng nhau, nghĩa là:

(f (x) = a_nx ^ n + a_ {n-1} x ^ {n-1} +… + a_1x + a_0 )

Với (a_i = a_ {ni} ) với (i = 0; 1; 2;…; n )

Ví dụ: (ax ^ 4 + bx ^ 3 + cx ^ 2 + bx + a = 0 ) là phương trình đối xứng bậc (4 )

(ax ^ 3 + bx ^ 2 + bx + a = 0 ) là một phương trình hệ số đối xứng của bậc (3 )

• Phương trình hệ số đối xứng bậc chẵn có nghiệm (x_0 ) thì (x_0 neq 0 ) và cũng nhận ( frac {1} {x_0} ) làm nghiệm.

• Phương trình hệ số đối xứng bậc lẻ luôn có thể được phân tích thành: ((x + 1) .f (x) ) trong đó (f (x) ) là phương trình hệ số đối xứng bậc chẵn.

Vì vậy:

• Phương trình đối xứng bậc lẻ luôn có nghiệm (x = -1 )

• Giải một phương trình đối xứng bậc lẻ được rút gọn thành một giải một phương trình đối xứng bậc chẵn.

Vì giải phương trình đối xứng bậc lẻ là nghiệm của phương trình đối xứng bậc chẵn nên ở đây ta chỉ xét cách giải phương trình đối xứng bậc chẵn:

(f (x) = a_nx ^ n + a_ {n-1} x ^ {n-1} +… + a_1x + a_0 ) trong đó (n ) chẵn

• Bước 1:

  Vì (x = 0 ) không phải là nghiệm của phương trình, hãy chia cả hai vế của phương trình cho (x ^ { frac {n} {2}} )

• Bước 2:

  Đặt (t = x + frac {1} {x} ) với điều kiện (| t | geq 2 ), biến phương trình thu được thành phương trình ẩn (t )

• Bước 3:

  Sau khi tìm được (t ), hãy giải phương trình (t = x + frac {1} {x} ) để tìm (x )

Giải phương trình: (3x ^ 4 + 7x ^ 3 + 7x + 3 = 0 )

Vì (x = 0 ) không phải là nghiệm của phương trình, hãy chia cả hai vế của phương trình cho (x ^ 2 ) để được:

(3x ^ 2 + 7x + frac {7} {x} + frac {3} {x ^ 2} = 0 )

( Leftrightarrow 3 (x ^ 2 + frac {1} {x ^ 2}) + 7 (x + frac {1} {x}) = 0 )

( Leftrightarrow 3 (x + frac {1} {x}) ^ 2-6 + 7 (x + frac {1} {x}) = 0 )

Đặt (t = x + frac {1} {x} ). Điều khoản: (| t | geq 2 )

Phương trình đã cho tương đương với:

(3t ^ 2 + 7t-6 = 0 Mũi tên trái (t + 3) (3t-2) = 0 )

( Leftrightarrow left[begin{array}{l}t=-3 \ t=frac{3}{2}end{array}right.)

Do (|t| geq 2) nên ( t=-3 )

Vậy ta có:

(x+frac{1}{x}=-3 Leftrightarrow x^2+3x+1=0)

(Leftrightarrow left[begin{array}{l} x= frac{-3+sqrt{5}}{2}\x=frac{-3-sqrt{5}}{2} end{array}right.)

Xem chi tiết qua bài giảng dưới đây nhé:

(Nguồn: www.youtube.com)

Xem thêm >>> Chuyên đề Hệ phương trình cơ bản và nâng cao

Các khoa liên quan:

• Hệ phương trình không đối xứng là gì?

• hệ phương trình đối xứng loại 2 lớp 9

Xem thêm bài viết thuộc chuyên mục: Giáo Dục