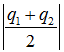Giải phương trình bằng cách đặt ẩn phụ giải phương trình chứa căn lớp 10

Phương pháp giải phương trình chứa ẩn dưới dấu căn bậc hai

Kỹ thuật đặt ẩn phụ đưa về phương trình thuần nhất bậc hai hai biến

Phương pháp

Giải phương trình : USD { { u } ^ { 2 } } + \ alpha uv + \ beta { { v } ^ { 2 } } = 0 USD ( 1 ) bằng cách

• Xét $v\ne 0$ phương trình trở thành  : ${{\left( \frac{u}{v} \right)}^{2}}+\alpha \left( \frac{u}{v} \right)+\beta =0$
• $v=0$ thử trực tiếp

Các trường hợp sau cũng đưa về được ( 1 )

• $a.A\left( x \right)+bB\left( x \right)=c\sqrt{A\left( x \right).B\left( x \right)}$
• $\alpha u+\beta v=\sqrt{m{{u}^{2}}+n{{v}^{2}}}$

*$Q\left( x \right)=\alpha \sqrt{P\left( x \right)}$ với:$\left\{ \begin{align}
& P\left( x \right)=A\left( x \right).B\left( x \right) \\
& Q\left( x \right)=aA\left( x \right)+bB\left( x \right) \\
\end{align} \right.$

Bằng cách thay các biểu thức A(x), B(x)  bởi các  biểu thức vô tỉ thì sẽ nhận được phương trình vô tỉ theo dạng này .

Phương trình dạng : $a.A\left( x \right)+bB\left( x \right)=c\sqrt{A\left( x \right).B\left( x \right)}$

Ví dụ 1.

Giải phương trình : USD 2 \ left ( { { x } ^ { 2 } } + 2 \ right ) = 5 \ sqrt { { { x } ^ { 3 } } + 1 } USD

Giải:

Điều kiện : USD x \ ge – 1 USD .
Nhận xét : USD { x ^ 3 } + 1 = \ left ( { x + 1 } \ right ) \ left ( { { x ^ 2 } – x + 1 } \ right ) USD
Vậy : USD A ( x ) = x + 1 USD và $ B ( x ) = { x ^ 2 } – x + 1 USD
Đặt USD u = \ sqrt { x + 1 }, v = \ sqrt { { { x } ^ { 2 } } – x + 1 } USD
Phương trình trở thành :
USD 2 \ left ( { { u ^ 2 } + { v ^ 2 } } \ right ) = 5 uv USD

Do:
$\begin{array}{l}
v = \sqrt {{x^2} – x + 1} \\
= \sqrt {\left( {{x^2} – 2.x.\frac{1}{2} + \frac{1}{4}} \right) + \frac{3}{4}} \\
= \sqrt {{{\left( {{x^2} – \frac{1}{2}} \right)}^2} + \frac{3}{4}} \ge \frac{{\sqrt 3 }}{2} > 0,\forall x
\end{array}$

Nên : USD v \ ne 0, \ forall x USD. Chia hai vế cho : USD { v ^ 2 } \ ne 0 USD

$PT \Leftrightarrow 2{\left( {\frac{u}{v}} \right)^2} – 5\left( {\frac{u}{v}} \right) + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}
u = 2v\\
u = \frac{1}{2}v
\end{array} \right.$

$\begin{align}
& *u=2v \\
& \Leftrightarrow \sqrt{x+1}=2\sqrt{{{x}^{2}}-x+1} \\
& \Leftrightarrow x+1=4({{x}^{2}}-x+1) \\
& \Leftrightarrow 4{{x}^{2}}-5x+3=0.(VN) \\
\end{align}$

$\begin{align}
& *u=\frac{1}{2}v \\
& \Leftrightarrow 2\sqrt{x+1}=\sqrt{{{x}^{2}}-x+1} \\
& \Leftrightarrow 4(x+1)={{x}^{2}}-x+1 \\
& \Leftrightarrow {{x}^{2}}-5x+-3=0 \\
& \Leftrightarrow x=\frac{5\pm \sqrt{37}}{2} \\
\end{align}$

Vậy phương trình có nghiệm : USD x = \ frac { 5 \ pm \ sqrt { 37 } } { 2 } USD

Ví dụ 2. 

Giải phương trình sau : USD 2 { { x } ^ { 2 } } + 5 x – 1 = 7 \ sqrt { { { x } ^ { 3 } } – 1 } USD

Giải

Điều kiện : USD x \ ge 1 USD
Nhận xét : Ta viết : USD \ alpha \ left ( x-1 \ right ) + \ beta \ left ( { { x } ^ { 2 } } + x + 1 \ right ) = 7 \ sqrt { \ left ( x-1 \ right ) \ left ( { { x } ^ { 2 } } + x + 1 \ right ) } USD
Đồng nhất thức ta được : USD 3 \ left ( x-1 \ right ) + 2 \ left ( { { x } ^ { 2 } } + x + 1 \ right ) = 7 \ sqrt { \ left ( x-1 \ right ) \ left ( { { x } ^ { 2 } } + x + 1 \ right ) } USD Đặt USD u = x-1 \ ge 0, v = { { x } ^ { 2 } } + x + 1 > 0 USD, ta được :

$3u+2v=7\sqrt{uv}\Leftrightarrow \left[ \begin{align}
& v=9u \\
& v=\frac{1}{4}u \\
\end{align} \right.$

$\begin{align}
& *v=9u \\
& \Leftrightarrow 9\left( x-1 \right)={{x}^{2}}+x+1 \\
& \Leftrightarrow {{x}^{2}}-8x-8=0 \\
& \Leftrightarrow x=4\pm \sqrt{6} \\
\end{align}$

$\begin{array}{l}
*u = 4v\\
\Leftrightarrow x – 1 = 4\left( {{x^2} + x + 1} \right)\\
\Leftrightarrow 4{x^2} + 3x + 5 = 0.(VN)
\end{array}$

Vậy phương trình có nghiêm : USD x = 4 \ pm \ sqrt { 6 } USD .

Ví dụ 3.

Giải phương trình : USD { { x } ^ { 3 } } – 3 { { x } ^ { 2 } } + 2 \ sqrt { { { \ left ( x + 2 \ right ) } ^ { 3 } } } – 6 x = 0 USD

Giải

Nhận xét : Đặt USD y = \ sqrt { x + 2 } USD ta hãy biến pt trên về phương trình thuần nhất bậc 3 so với x và y :

$\begin{array}{l}
{x^3} – 3{x^2} + 2{y^3} – 6x = 0\\
\Leftrightarrow {x^3} – 3x{y^2} + 2{y^3} = 0\\
\Leftrightarrow {\left( {\frac{x}{y}} \right)^3} – 3\left( {\frac{x}{y}} \right) + 2 = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = y\\
x = – 2y
\end{array} \right.
\end{array}$

Vậy phương trình có nghiệm : USD x = 2, x = 2-2 \ sqrt { 3 } USD .

Phương trình dạng :  $\alpha u+\beta v=\sqrt{m{{u}^{2}}+n{{v}^{2}}}$

Bình phương hai vế thì đưa phương trình về được dạng :
USD a. A \ left ( x \ right ) + bB \ left ( x \ right ) = c \ sqrt { A \ left ( x \ right ). B \ left ( x \ right ) } USD .

Ví dụ 1.  

giải phương trình : ${{x}^{2}}+3\sqrt{{{x}^{2}}-1}=\sqrt{{{x}^{4}}-{{x}^{2}}+1}$

Giải:

Ta đặt :

$\left\{ \begin{array}{l}
u = {x^2}\\
v = \sqrt {{x^2} – 1}
\end{array} \right.$

khi đó phương trình trở thành : USD u + 3 v = \ sqrt { { { u } ^ { 2 } } – { { v } ^ { 2 } } } USD

Ví dụ 2.

Giải phương trình sau : USD \ sqrt { { { x } ^ { 2 } } + 2 x } + \ sqrt { 2 x – 1 } = \ sqrt { 3 { { x } ^ { 2 } } + 4 x + 1 } USD

Giải

Điều kiện : USD x \ ge \ frac { 1 } { 2 } USD .
Bình phương 2 vế ta có :

$\begin{array}{l}
\sqrt {\left( {{x^2} + 2x} \right)\left( {2x – 1} \right)} = {x^2} + 1\\
\Leftrightarrow \sqrt {\left( {{x^2} + 2x} \right)\left( {2x – 1} \right)} = \left( {{x^2} + 2x} \right) – \left( {2x – 1} \right)
\end{array}$

Ta hoàn toàn có thể đặt :

$\left\{ \begin{align}
& u={{x}^{2}}+2x \\
& v=2x-1 \\
\end{align} \right.$

khi đó ta có hệ :

$uv = {u^2} – {v^2} \Leftrightarrow \left[ \begin{array}{l}
u = \frac{{1 – \sqrt 5 }}{2}v\\
u = \frac{{1 + \sqrt 5 }}{2}v
\end{array} \right.$

Do USD u, v \ ge 0 USD. USD u = \ frac { 1 + \ sqrt { 5 } } { 2 } v \ Leftrightarrow { { x } ^ { 2 } } + 2 x = \ frac { 1 + \ sqrt { 5 } } { 2 } \ left ( 2 x – 1 \ right ) USD

Ví dụ 3. 

Giải phương trình : USD \ sqrt { 5 { { x } ^ { 2 } } – 14 x + 9 } – \ sqrt { { { x } ^ { 2 } } – x-20 } = 5 \ sqrt { x + 1 } USD

Giải:

Điều kiện : USD x \ ge 5 USD .
Chuyển vế bình phương ta được : USD 2 { { x } ^ { 2 } } – 5 x + 2 = 5 \ sqrt { \ left ( { { x } ^ { 2 } } – x-20 \ right ) \ left ( x + 1 \ right ) } USD

Nhận xét :   không tồn tại số $\alpha ,\beta $ để : $2{{x}^{2}}-5x+2=\alpha \left( {{x}^{2}}-x-20 \right)+\beta \left( x+1 \right)$ vậy ta không thể đặt:

$\left\{ \begin{array}{l}
u = {x^2} – x – 20\\
v = x + 1
\end{array} \right.$

Để xử lý yếu tố này, ta có : USD \ left ( { { x } ^ { 2 } } – x-20 \ right ) \ left ( x + 1 \ right ) = \ left ( x + 4 \ right ) \ left ( x-5 \ right ) \ left ( x + 1 \ right ) = \ left ( x + 4 \ right ) \ left ( { { x } ^ { 2 } } – 4 x – 5 \ right ) USD .
Ta viết lại phương trình : USD 2 \ left ( { { x } ^ { 2 } } – 4 x – 5 \ right ) + 3 \ left ( x + 4 \ right ) = 5 \ sqrt { ( { { x } ^ { 2 } } – 4 x – 5 ) ( x + 4 ) } USD .
Đến đây bài toán được xử lý .

Sáng tạo

Xuất phát từ đẳng thức :

•  ${{x}^{3}}+1=\left( x+1 \right)\left(
  {{x}^{2}}-x+1 \right)$
• ${{x}^{4}}+{{x}^{2}}+1=\left(
  {{x}^{4}}+2{{x}^{2}}+1 \right)-{{x}^{2}}=\left( {{x}^{2}}+x+1
  \right)\left( {{x}^{2}}-x+1 \right)$
• ${{x}^{4}}+1=\left(
  {{x}^{2}}-\sqrt{2}x+1 \right)\left( {{x}^{2}}+\sqrt{2}x+1 \right)$
• $4{{x}^{4}}+1=\left(
  2{{x}^{2}}-2x+1 \right)\left( 2{{x}^{2}}+2x+1 \right)$

Hãy tạo ra những phương trình vô tỉ dạng trên ví dụ như : USD 4 { { x } ^ { 2 } } – 2 \ sqrt { 2 } x + 4 = \ sqrt { { { x } ^ { 4 } } + 1 } USD
Để có một phương trình đẹp, cần chú ý quan tâm chọn thông số a, b, c sao cho phương trình bậc hai USD a { { t } ^ { 2 } } + bt-c = 0 USD giải có “ nghiệm đẹp ” .

Bài tập thực hành

— — — — — — — — –
Download tài liệu :
PDF : tại đây .

— — — — — — — — –Download tài liệu :PDF : tại đây .

Word: tại đây.

— — — — — — — — –

Xem thêm:

— — — — — — — –