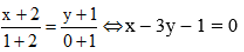
Bài tập ôn tập chương 1 hình học 111 là tâm huyết biên soạn của đội ngũ giáo viên dạy giỏi môn toán giúp các em học tốt môn toán hình 11. Bài tập ôn tập chương 1 giúp các em ôn tập lại các dạng bài tập trong phần chương 1 hình học 11.
thuộc:
Hướng dẫn giải bài tập ôn tập chương 1 hình học 11
thuộc: Chương I: Phép dời hình và phép đồng dạng trong mặt phẳng
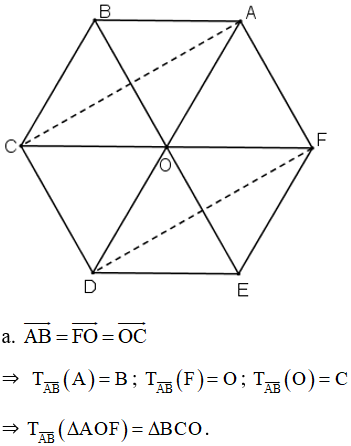
Bài 1 (trang 34 SGK Hình học 11): Cho lục giác đều ABCDEF tâm O. Tìm ảnh của tam giác AOF.
a. Qua phép tịnh tiến theo vectơ AB
b. Qua phép đối xứng qua đường thẳng BE.
c. Qua phép quay tâm O góc quay 120o.
Lời giải:
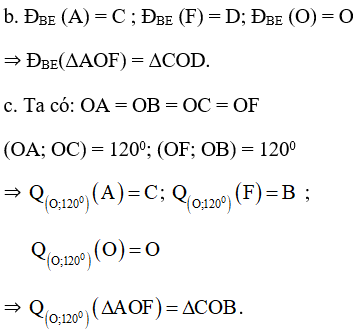
Bài 2 (trang 34 SGK Hình học 11): Trong mặt phẳng tọa độ Oxy cho điểm A(-1; 2) và đường thẳng d có phương trình 3x + y + 1 = 0. Tìm ảnh của A và d.
a. Qua phép tịnh tiến theo vectơ v = (2; 1);
b. Qua phép đối xứng trục Oy;
c. Qua phép đối xứng qua gốc tọa độ;
d. Qua phép quay tâm O góc 90o.
Lời giải:
Ta có: A(-1; 2) ∈ (d): 3x + y + 1 = 0.
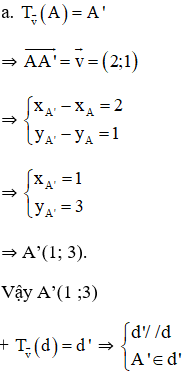
⇒ (d’): 3x + y – 6 = 0.
b. ĐOy (A) = A1 (1 ; 2)
Lấy B(0 ; -1) ∈ d
Ảnh của B qua phép đối xứng trục Oy: ĐOy (B) = B(0; -1) (vì B ∈ Oy).
⇒ d1 = ĐOy (d) chính là đường thẳng A1B.
⇒ d1: 3x – y – 1 = 0.
c. Phép đối xứng tâm O biến A thành A2(1; -2).
d2 là ảnh của d qua phép đối xứng tâm O
⇒ d2 // d và d2 đi qua A2(1 ; -2)
⇒ (d2): 3x + y – 1 = 0.
d. Gọi M(-1; 0) và N(0; 2) lần lượt là hình chiếu của A(-1; 2) trên Ox, Oy.
Q(O;90º) biến N thành N’(-2; 0), biến A thành A’, biến M thành B(0; -1).
Vậy Q(O;90º) biến hình chữ nhật ONAM thành hình chữ nhật ON’A’B. Do đó A’(-2; -1) đi qua A và B, Q(O;90º) biến A thành A’(-2; -1) biến B thành B’(1; 0)
Vậy Q(O;90º) biến d thành d’ qua hai điểm A’, B’
Do đó phương trình d’ là :
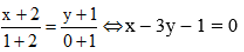
Bài 2 (trang 34 SGK Hình học 11): Trong mặt phẳng tọa độ Oxy cho điểm A(-1; 2) và đường thẳng d có phương trình 3x + y + 1 = 0. Tìm ảnh của A và d.
a. Qua phép tịnh tiến theo vectơ v = (2; 1);
b. Qua phép đối xứng trục Oy;
c. Qua phép đối xứng qua gốc tọa độ;
d. Qua phép quay tâm O góc 90o.
Lời giải:
Ta có: A(-1; 2) ∈ (d): 3x + y + 1 = 0.
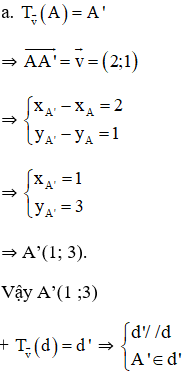
⇒ (d’): 3x + y – 6 = 0.
b. ĐOy (A) = A1 (1 ; 2)
Lấy B(0 ; -1) ∈ d
Ảnh của B qua phép đối xứng trục Oy: ĐOy (B) = B(0; -1) (vì B ∈ Oy).
⇒ d1 = ĐOy (d) chính là đường thẳng A1B.
⇒ d1: 3x – y – 1 = 0.
c. Phép đối xứng tâm O biến A thành A2(1; -2).
d2 là ảnh của d qua phép đối xứng tâm O
⇒ d2 // d và d2 đi qua A2(1 ; -2)
⇒ (d2): 3x + y – 1 = 0.
d. Gọi M(-1; 0) và N(0; 2) lần lượt là hình chiếu của A(-1; 2) trên Ox, Oy.
Q(O;90º) biến N thành N’(-2; 0), biến A thành A’, biến M thành B(0; -1).
Vậy Q(O;90º) biến hình chữ nhật ONAM thành hình chữ nhật ON’A’B. Do đó A’(-2; -1) đi qua A và B, Q(O;90º) biến A thành A’(-2; -1) biến B thành B’(1; 0)
Vậy Q(O;90º) biến d thành d’ qua hai điểm A’, B’
Do đó phương trình d’ là :
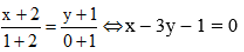
Bài 3 (trang 34 SGK Hình học 11): Trong mặt phẳng tọa độ Oxy, cho đường tròn tâm I(3 ; -2), bán kính 3.
a. Viết phương trình của đường tròn đó.
b. Viết phương trình ảnh của đường tròn (I ; 3) qua phép tịnh tiến theo vectơ v = (-2 ; 1).
c. Viết phương trình ảnh của đường tròn (I ; 3) qua phép đối xứng trục Ox.
d. Viết phương trình ảnh của đường tròn (I ; 3) qua phép đối xứng qua gốc tọa độ.
Lời giải:
a. Phương trình đường tròn : (x – 3)2 + (y + 2)2 = 9.
b. (I1; R1) là ảnh của (I; 3) qua phép tịnh tiến theo vec tơ v.
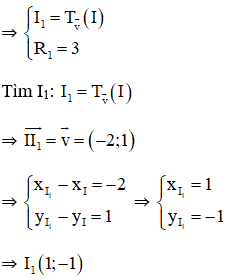
⇒ Phương trình đường tròn cần tìm: (x – 1)2 + ( y + 1)2 = 9.
c. (I2; R2) là ảnh của (I; 3) qua phép đối xứng trục Ox
⇒ R2 = 3 và I2 = ĐOx(I)
Tìm I2: I2 = ĐOx(I) ⇒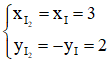 
⇒ I2(3; 2)
⇒ Phương trình đường tròn cần tìm: (x – 3)2 + (y – 2)2 = 9.
d. (I3; R3) là ảnh của (I; 3) qua phép đối xứng qua gốc O.
⇒ R3 = 3 và I3 = ĐO(I)
Tìm I3: I3 = ĐO(I) ⇒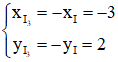 
⇒ Phương trình đường tròn cần tìm: (x + 3)2 +(y – 2)2 = 9.
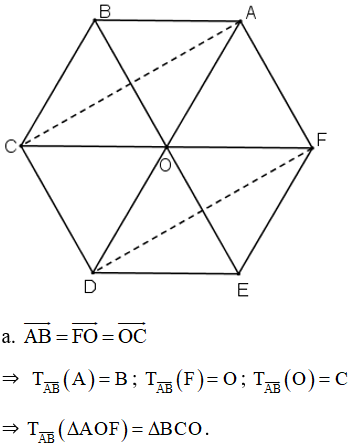
Bài 4 (trang 34 SGK Hình học 11): Cho lục giác đều ABCDEF tâm O. Tìm ảnh của tam giác AOF.
a. Qua phép tịnh tiến theo vectơ AB
b. Qua phép đối xứng qua đường thẳng BE.
c. Qua phép quay tâm O góc quay 120o.
Lời giải:
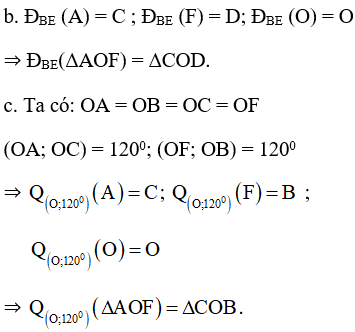
Bài 5 (trang 35 SGK Hình học 11): Cho hình chữ nhật ABCD. Gọi O là tâm đối xứng của nó. Gọi I, F, J, E lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Tìm ảnh của tam giác AEO qua phép đồng dạng có được từ việc thực hiện liên tiếp phép đối xứng qua đường thẳng IJ và phép vị tự tâm B, tỉ số 2.
Lời giải:
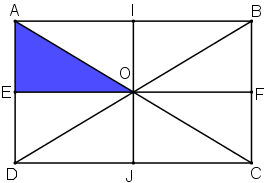
+ Lấy đối xứng qua đường thẳng IJ.
IJ là đường trung trực của AB và EF
⇒ ĐIJ(A) = B; ĐIJ (E) = F
O ∈ IJ ⇒ ĐIJ (O) = O
⇒ ĐIJ (ΔAEO) = ΔBFO
+ ΔBFO qua phép vị tự tâm B tỉ số 2
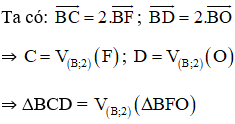
Vậy ảnh của ΔAEO qua phép đồng dạng theo đề bài là ΔBCD.
Bài 6 (trang 35 SGK Hình học 11): Trong mặt phẳng tọa độ Oxy, cho đường tròn tâm I(1; -3), bán kính 2. Viết phương trình ảnh của đường tròn (I; 2) qua phép đồng dạng có đưuọc từ việc thực hiện liên tiếp phép vị tự tâm O tỉ số 3 và phép đối xứng qua trục Ox.
Lời giải:
+ Gọi (I1; R1) là ảnh của (I; 2) qua phép vị tự tâm O, tỉ số 3.
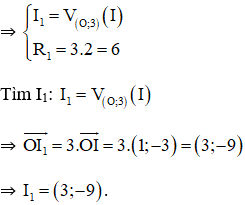
+ Gọi (I2; R2) là ảnh của (I1; R1) qua phép đối xứng trục Ox
⇒ R2 = R1 = 6.
I2 đối xứng với I1 qua Ox ⇒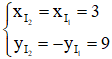 
⇒ I2(3; 9)
Vậy (I2; R2) chính là ảnh của (I; 2) qua phép đồng dạng trên và có phương trình: (x – 3)2 + (y – 9)2 = 36.
Bài 7 (trang 35 SGK Hình học 11): Cho hai điểm A, B và đường tròn tâm O không có điểm chung với đường thẳng AB. Qua mỗi điểm M chạy trên đường tròn (O) dựng hình bình hành MABN. Chứng minh rằng điểm N thuộc một đường tròn xác định.
Lời giải:
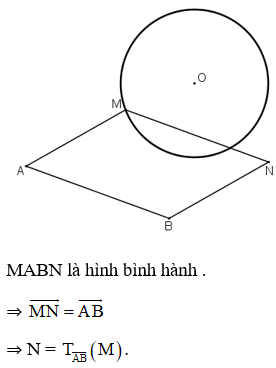
Vậy khi M di chuyển trên đường tròn (O; R) thì N di chuyển trên đường tròn (O’ ; R) là ảnh của (O ; R) qua phép tịnh tiến theo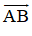 
Bài tập ôn tập chương 1 hình học 11 được biên soạn bám sát theo chương trình SGK mới toán hình lớp 11. Được Soanbaitap.com chia sẻ và đăng trong chuyên mục giải toán 11 giúp các em tiện tra cứu và tham khảo để học toán 11. Nếu thấy hay hãy comment và chia sẻ để nhiều bạn khác cùng học tập.
Ôn tập Hình 11 chương 1 Phép biến hình – Thầy Nguyễn Công Chính
https://www.facebook.com/thaychinhdaytoan
phép biến hình đồng dạng mặt phẳng
