Phương Trình Parabol Có Dạng Gì, Hàm Số Bậc 2 Và Ứng Dụng Trong Giải Toán – Lingocard.vn
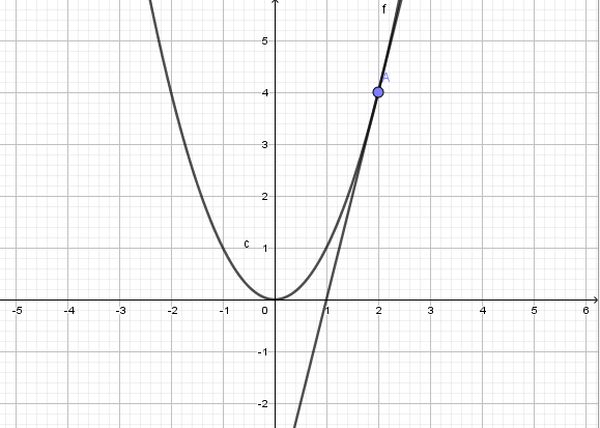
Phương Trình Parabol Có Dạng Gì, Hàm Số Bậc 2 Và Ứng Dụng Trong Giải Toán
Phương Trình Parabol Có Dạng Gì, Hàm Số Bậc 2 Và Ứng Dụng Trong Giải Toán
Trong môn toán đại số Parabol chính là phương trình được gặp rất nhiều trong môn toán. Parabol cũng chính là nguyên nhân khiến bao nhiêu thế hệ học sinh đau đầu vì bài tập cũng như phương pháp vẽ Parabol. Nội dung sau đây lingocard.vn sẽ gửi đến bạn những tri thức thiết yếu liên quan đến Parabol. Các bạn hãy cùng tham khảo nhé!
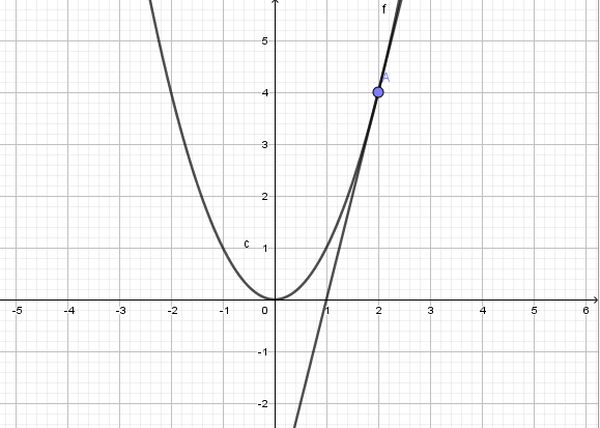
Parabol chính là tri thức trọng yếu và vô cùng thiết yếu trong môn toán
Table of Contents
Đường Parabol là gì?
Trong toán học, parabol (Tiếng Anh là parabola, bắt nguồn từ tiếng Hy Lạp παραβολή) là một đường conic được tạo bởi giao của một hình nón và một mặt phẳng song song với đường sinh của hình đó. Một parabol cũng có thế được khái niệm như một tập hợp các điểm trên mặt phẳng cách đều một điểm cho trước (tiêu điểm) và một đường thẳng cho trước (đường chuẩn).
Đang xem: Phương trình parabol có dạng gì
Trường hợp đặc biệt xảy ra khi mặt phẳng cắt tiếp xúc với mặt conic. Trong trường hợp này, giao tuyến sẽ suy biến thành một đường thẳng.
Parabol là một khái niệm trọng yếu trong toán học trừu tượng. Tuy nhiên, nó cũng được bắt gặp với tần suất cao trong toàn cầu vật lý, và có nhiều ứng dụng trong kỹ thuật, vật lý, và các ngành nghề khác.
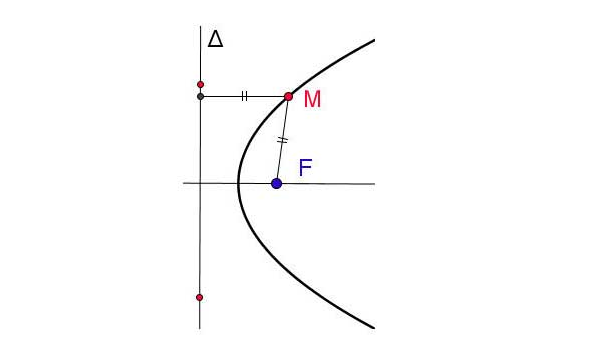
ho một điểm F cố định và một đường thẳng cố định không đi qua F. Tập hợp các điểm M cách đều F và được gọi là đường parabol (hay parabol).
Điểm F được gọi là tiêu điểm của parabol.
Đường thẳng được gọi là đường chuẩn của parabol.
Khoảng cách từ F đến được gọi là tham số tiêu của parabol.
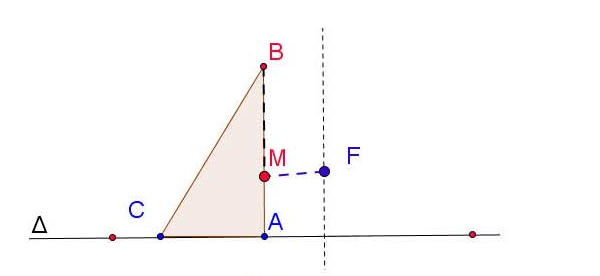
Ta có thể vẽ parabol với tiêu điểm F và đường chuẩn như sau: Lấy một êke ABC (vuông ở A) và một đoạn dây không đàn hồi, có độ dài bằng AB. Đính một đầu dây vào điểm F, đầu kia vào đỉnh B của êke. Đặt êke sao cho cạnh AC nằm trên , lấy đầu bút chì ép sát sợi dây rồi cho cạnh AC của êke trượt trên . Khi đó đầu M của bút chì sẽ vạch nên một phần của parabol (vì ta luôn có MF = MA).
Hãy cùng tham khảo video sau đây để hiểu thế nào là parabol nhé!
Khái niệm phương trình Parabol
Phương trình Parabol được trình diễn như sau: y = a^2+bx+c
Hoành độ của đỉnh là (-b)/ (2a)
Thay tọa độ trục hoành vào phương trình, ta tìm được hoành độ Parabol có công thức dưới dạng: ( (b^2) – 4ac) / 4a
Phương trình chính tắc của Parabol
Phương trình chính tắc của parabol được trình diễn dưới dạng:
Phương trình chính tắc của parabol
Cho parabol với tiêu điểm F và đường chuẩn Delta.
Ta chọn hệ trục tọa độ Oxy sao cho O là trung điểm của FP và điểm F nằm trên tia Ox.
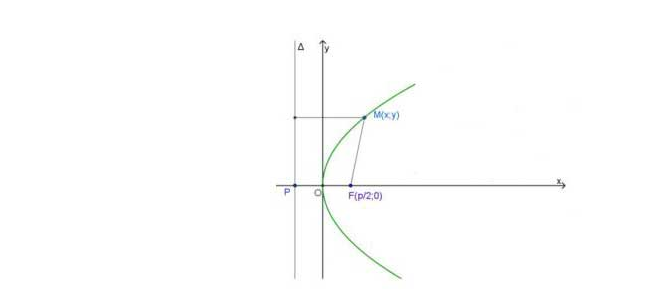

Note: Ở môn đại số, tất cả chúng ta gọi đồ thị của hàm số bậc hai y = ax^2 + bx + c là một đường parabol.
Cách xác nhận tọa độ đỉnh của parabol
Ví dụ: Xác nhận tọa độ của đỉnh và các giao điểm với trục tung, trục hoành (nếu có) của mỗi parabol.
Xem thêm: Đồ Án Thiết Kế Hệ Thống Lạnh, Đồ Án Thiết Kế Hệ Thống Điều Hòa Không Khí
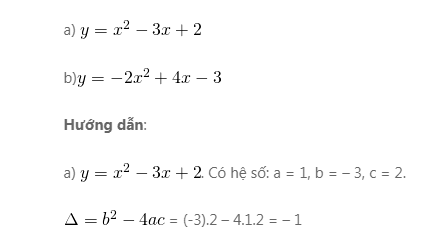
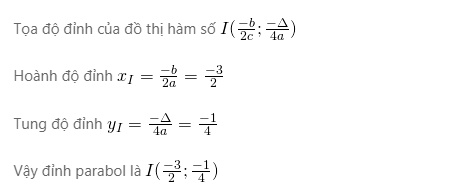

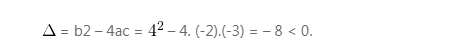
Phương trình vô nghiệm ⇒ không tồn tại giao điểm của hàm số với trục hoành.
Cách lập phương trình Parabol
Cho hàm số y = ax^2
Hàm số này xác nhận trên R :
Nếu a > 0 thì hàm số giảm trên (-∞ ; 0) ; tăng trên (0;+ ∞ ),đạt cực tiểu khi x = 0
Nếu a
Đồ thị Parabol của hàm số y = ax^ 2 có đỉnh là gốc O và trục đối xứng là Oy.
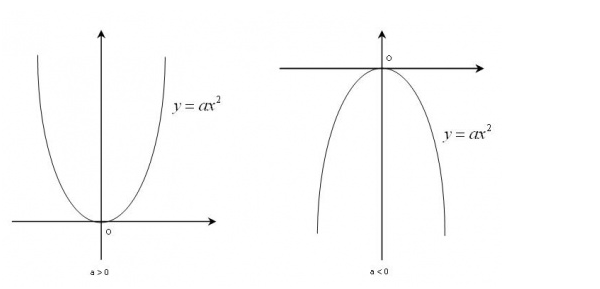
Parabol có tọa độ đỉnh O(0;0)
Sự tương giao giữa đường thẳng và Parabol
Sự tương giao giữa đường thẳng d: y = mx + n và parabol (P): y = a ^2 (a khác 0)
Số giao điểm của đường thẳng d và parabol (P) là số nghiệm của phương trình hoành độ giao điểm
+) Phương trình (*) có hai nghiệm phân biệt thì d cắt (P) tại hai điểm phân biệt
+) Phương trình (*) có nghiệm kép thì d tiếp xúc với (P)
+) Phương trình (*) vô nghiệm thì d không cắt (P).
Ví dụ parabol
Xác nhận parabol y = ax ^2 + bx + 2, biết rằng parabol đó:
a) Đi qua hai điểm M(1; 5) và N(- 2; 8);b) Đi qua hai điểm A(3;- 4) và có trục đối xứng là x=-3/2c) Có đỉnh là I(2;- 2);d) Đi qua điểm B(- 1; 6) và tung độ của đỉnh là -1/4a) M(1; 5) ∈ (P) nên tọa độ của M thỏa mãn parabol:yM = (axM) ^2 + bxM + 2 ↔ 5 = a.12 + b.1 + 2. (1)
N(- 2; 8) ∈ (P) nên tọa độ của N thỏa mãn parabol:yN = (axN) ^2 + bxN + 2 ↔ 8 = a.(- 2)2 + b.(- 2) + 2 (2)
Giải hệ phương trình:(1) và (2) ta được a = 2, b = 1.
Vậy Parabol có phương trình là: y = 2×2 + x + 2.
b) Đi qua điểm A(3;- 4) và có trục đối xứng là x=-3/2
A(3;- 4) ∈ (P) nên tọa độ của A thỏa mãn parabol:yA = (axA) ^2 + bxA + 2 ↔ -4 = a.3 ^2 + b.3 + 2 (1)
y = ax ^2 + bx + 2 có trục đối x = -b/2a ↔ -3/2 = -b/2a ↔ b = 3a (2)
Giải hệ phương trình (1) và (2) ta có a = -1/3, b = -1
Parabol: y = -1/3x ^2 – x + 2.
c) Cho hàm số y = ax ^ 2 + bx + 2
Tọa độ đỉnh của hàm số là I(-b/2a; -Δ/4a). Theo đề bài cho tọa độ đỉnh là I(2;- 2)
-b/2a = 2 ↔ -b = 4a (1)
-Δ/4a = – 2 ↔ -(b2 – 8a )= -8a (2)
Giải hệ phương trình (1) và (2) ta thu được kết quả là b = 0 và b = -4
với b = 0 → a = 0 → y = 2 là 1 đường thẳng (loại)
với b = -4 → a = 1
Tổng kết Parabol cần tìm là Parabol: y = (x)^2 – 4x + 2.
d) Đi qua điểm B(- 1; 6) và tung độ của đỉnh là -1/4
B(- 1; 6) ∈ (P) nên tọa độ của B thỏa mãn parabol:yB = (axB)^2 + bxB + 2 ↔ 6 = a.(-1)2 + b.(-1) + 2
Tọa độ đỉnh I(-b/2a; -Δ/4a) tung độ của tọa độ đỉnh là yI = -Δ/4a = -1/4 ↔ – (b2 – 8a )= -a (2)
Giải hệ phương trình (1) và (2) thu được kết quả
a = 16 →b = 12
a = 1 → b = -3
Parabol: y = 16x ^2 + 12x + 2 hoặc y = x2 – 3x + 2.
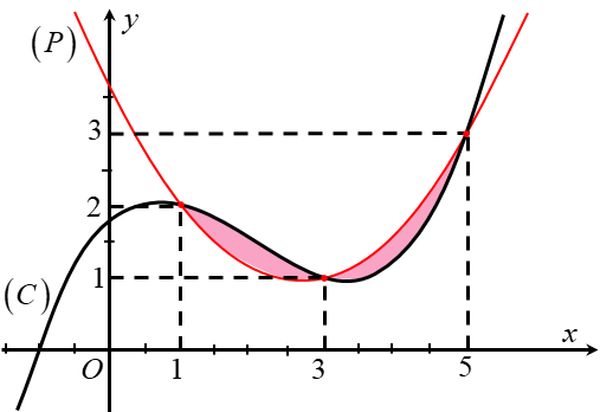
Đồ thi parabol khi trổ tài trên hệ trục tọa độ
Các bài tập về parabol
Bài 1: Cho Parabol (P): y = 2x ^2
a) Vẽ đồ thị hàm (P)b) Tìm giao điểm của (P) với đường thẳng y = 2x+1.
Bài 2: Cho (P): Y = 1/ 2X^2 và đường thẳng (d); y = ax+b.
Xem thêm: Share Khóa Học Tiếng Anh Cực Khủng Đầy Đủ Từ A, Share Khoá Học Nói Tiếng Anh Tự Tin Trong 3 Tháng
a) Xác nhận điểm a và b để đường thẳng (d) đi qua A(-1;0) và tiếp xúc với (P).b) Tìm tọa độ tiếp điểm.
Nội dung trên đã gửi đến bạn những tri thức liên quan đến parabol cũng như những tri thức thú vị liên quan đến parabol. Kì vọng nội dung trên có thể giúp ích được cho bạn. Parabol là tri thức vô cùng trọng yếu trong môn toán đại số. Vậy nên các bạn nhất định phải ghi nhớ những tri thức trên nhé!
Xem thêm nội dung thuộc thể loại: Phương trình




