Giải bài 43, 44, 45, 46, 47, 48, 49, 50 trang 47, 48 sgk đại số và giải tích 11 nâng cao

Bạn đang xem: Giải bài 43, 44, 45, 46, 47, 48, 49, 50 trang 47, 48 sgk đại số và giải tích 11 nâng cao Tại Website vuongquocdongu.com

Câu 43 trang 47 SGK Đại số và Giải tích 11 Nâng cao

Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai ?

a. Các hàm số \(y = \sin x, y = \cos x\) có cùng tập xác định.

b. Các hàm số \(y = \tan x, y = \cot x\) có cùng tập xác định.

c. Các hàm số \(y = \sin x, y = \tan x\) là những hàm số lẻ.

d. Các hàm số \(y = \cos x, y = \cot x\) là những hàm số chẵn.

e. Các hàm số \(y = \sin x, y = \cos x\) cùng nghịch biến trên khoảng  \(\left( {{\pi \over 2};{{3\pi } \over 2}} \right)\)

f. Hàm số \(y = \cos x\) nghịch biến trên khoảng \((-2π ; -π)\)

g. Trên mỗi khoảng mà hàm số \(y = \tan x\) đồng biến thì hàm số \(y = \cot x\) nghịch biến.

Giải

a. Đúng vì hàm số \(y = \sin x, y = \cos x\) có cùng tập xác định \(D =\mathbb R\)

b. Sai vì \(y = \tan x\) xác định \(∀x \ne {\pi \over 2} + k\pi \) còn \(y = \cot x\) xác định \(∀x ≠ kπ\)

c. Đúng

d. Sai vì \(y = \cot x\) là hàm số lẻ.

e. Sai vì \(y = \cos x\) không nghịch biến trên khoảng  \(\left( {{\pi \over 2};{{3\pi } \over 2}} \right)\)

f. Đúng

g. Sai vì trên khoảng \(\left( { – {\pi \over 2};{\pi \over 2}} \right)\) hàm số \(y = \tan x\) đồng biến nhưng hàm số \(y = \cot x\) không nghịch biến.

 

Câu 44 trang 47 SGK Đại số và Giải tích 11 Nâng cao

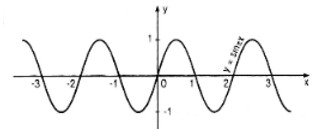
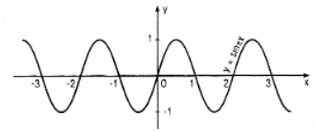
Xét hàm số \(y = f(x) = \sinπx\).

a. Chứng minh rằng với mỗi số nguyên chẵn \(m\) ta có \(f(x + m) = f(x)\) với mọi \(x\).

b. Lập bảng biến thiên của hàm số trên đoạn \([-1 ; 1]\).

c. Vẽ đồ thị của hàm số đó.

Giải:

a. Đặt \(m = 2k, k \in\mathbb Z\). Ta có :

\(f(x + m) = \sinπ(x + m) = \sin(πx + 2kπ) = \sinπx = f(x)\)

b. Bảng biến thiên

 

c. Đồ thị

 

Câu 45 trang 47 SGK Đại số và Giải tích 11 Nâng cao

Đưa các biểu thức sau về dạng \(C\sin(x + α)\) :

a.  \(\sin x + \tan {\pi \over 7}\cos x\)

b.  \(\tan {\pi \over 7}\sin x + \cos x\)

Giải

a. Ta có:

\(\eqalign{
& \sin x + \tan {\pi \over 7}\cos x = \sin x + {{\sin {\pi \over 7}} \over {\cos {\pi \over 7}}}\cos x \cr
& = {1 \over {\cos {\pi \over 7}}}\left( {\sin x\cos {\pi \over 7} + \sin {\pi \over 7}\cos x} \right) \cr
& = {1 \over {\cos {\pi \over 7}}}\sin \left( {x + {\pi \over 7}} \right) \cr} \) 

b.

\(\eqalign{
& \tan {\pi \over 7}\sin x + \cos x = {{\sin {\pi \over 7}} \over {\cos {\pi \over 7}}}\sin x + \cos x \cr
& = {1 \over {\cos {\pi \over 7}}}\left( {\sin x\sin {\pi \over 7} + \cos x\cos {\pi \over 7}} \right) \cr
& = {1 \over {\cos {\pi \over 7}}}\cos \left( {x – {\pi \over 7}} \right) = {1 \over {\cos {\pi \over 7}}}\sin \left( {x – {\pi \over 7} + {\pi \over 2}} \right) \cr
& = {1 \over {\cos {\pi \over 7}}}\sin \left( {x + {{5\pi } \over {14}}} \right) \cr} \)

 

Câu 46 trang 48 SGK Đại số và Giải tích 11 Nâng cao

Giải các phương trình sau :

a.  \(\sin \left( {x – {{2\pi } \over 3}} \right) = \cos 2x\)

b.  \(\tan \left( {2x + 45^\circ } \right)\tan \left( {180^\circ – {x \over 2}} \right) = 1\)

c.  \(\cos 2x – {\sin ^2}x = 0\)

d.  \(5\tan x – 2\cot x = 3\)

Giải

a. Ta có:

\(\eqalign{& \sin \left( {x – {{2\pi } \over 3}} \right) = \cos 2x \cr & \Leftrightarrow \sin \left( {x – {{2\pi } \over 3}} \right) = \sin \left( {{\pi \over 2} – 2x} \right) \cr & \Leftrightarrow \left[ {\matrix{{x – {{2\pi } \over 3} = {\pi \over 2} – 2x + k2\pi } \cr {x – {{2\pi } \over 3} = \pi – {\pi \over 2} + 2x + k2\pi } \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{x = {{7\pi } \over {18}} + k{{2\pi } \over 3}} \cr {x = – {{7\pi } \over 6} – k2\pi } \cr} } \right. \cr} \)

b. Với ĐKXĐ của phương trình ta có \(\tan(2x + 45^0) = \cot(45^0 – 2x)\) và \(\tan \left( {180^\circ – {x \over 2}} \right) = \tan \left( { – {x \over 2}} \right)\) nên :

\(\eqalign{
& \tan \left( {2x + 45^\circ } \right)\tan \left( {180^\circ – {x \over 2}} \right) = 1 \cr
& \Leftrightarrow \cot \left( {45^\circ – 2x} \right)\tan \left( { – {x \over 2}} \right) = 1 \cr
& \Leftrightarrow \tan \left( { – {x \over 2}} \right) = \tan \left( {45^\circ – 2x} \right) \cr
& \Leftrightarrow – {x \over 2} = 45^\circ – 2x + k180^\circ \cr
& \Leftrightarrow x = 30^\circ + k120^\circ ,k \in\mathbb Z \cr} \)

c. Ta có:

\(\eqalign{
& \cos 2x – {\sin ^2}x = 0 \cr
& \Leftrightarrow \cos 2x – {{1 – \cos 2x} \over 2} = 0 \cr
& \Leftrightarrow 3\cos 2x – 1 = 0 \Leftrightarrow \cos 2x = {1 \over 3} \cr
& \Leftrightarrow \cos 2x = \cos \alpha \,\left( {\text{ với }\,\cos \alpha = {1 \over 3}} \right) \cr
& \Leftrightarrow x = \pm {\alpha \over 2} + k\pi \,\,(k\in\mathbb Z)\cr} \)

d.

\(\eqalign{& 5\tan x – 2\cot x = 3 \cr & \Leftrightarrow 5\tan x – {2 \over {\tan x}} = 3 \cr & \Leftrightarrow 3{\tan ^2}x – 3\tan x – 2 = 0 \cr & \Leftrightarrow \left[ {\matrix{{\tan x = 1} \cr {\tan x = – {2 \over 5}} \cr} } \right. \Leftrightarrow \left[ {\matrix{{x = {\pi \over 4} + k\pi } \cr {x = \alpha + k\pi } \cr}k\in\mathbb Z } \right. \cr & \text{trong đó}\,\tan \alpha = – {2 \over 5} \cr} \)

 

Câu 47 trang 48 SGK Đại số và Giải tích 11 Nâng cao

Giải các phương trình sau :

a.  \(\sin 2x + {\sin ^2}x = {1 \over 2}\)

b.  \(2{\sin ^2}x + 3\sin x\cos x + {\cos ^2}x = 0\)

c.  \({\sin ^2}{x \over 2} + \sin x – 2{\cos ^2}{x \over 2} = {1 \over 2}\)

Giải

Ta có:

\(\eqalign{
& \sin 2x + {\sin ^2}x = {1 \over 2} \cr
& \Leftrightarrow \sin 2x + {1 \over 2}\left( {1 – \cos 2x} \right) = {1 \over 2} \cr
& \Leftrightarrow \sin 2x – {1 \over 2}\cos 2x = 0 \cr
& \Leftrightarrow \tan 2x = {1 \over 2} \cr
& \Leftrightarrow 2x = \alpha + k\pi \,\text{ với }\,\tan \alpha = {1 \over 2} \cr
& \Leftrightarrow x = {\alpha \over 2} + k{\pi \over 2},\,k \in\mathbb Z \cr} \)

b.\(x = {\pi \over 2} + k\pi \) không là nghiệm phương trình.

Chia hai vế phương trình cho \({\cos ^2}x\) ta được :

\(\eqalign{& 2{\tan ^2}x + 3\tan x + 1 = 0 \Leftrightarrow \left[ {\matrix{{\tan x = – 1} \cr {\tan x = – {1 \over 2}} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{x = – {\pi \over 4} + k\pi } \cr {x = \alpha + k\pi } \cr} } \right.\,\left( {k \in\mathbb Z} \right) \cr & \left( {\text{ với }\,\tan \alpha = – {1 \over 2}} \right) \cr} \)

c. Ta có:

\(\eqalign{
& {\sin ^2}{x \over 2} + \sin x – 2{\cos ^2}{x \over 2} = {1 \over 2} \cr
& \Leftrightarrow {\sin ^2}{x \over 2} + 2\sin {x \over 2}\cos {x \over 2} – 2{\cos ^2}{x \over 2} = {1 \over 2} \cr} \) 

Với \(x\) mà \(\cos {x \over 2} = 0\) không là nghiệm phương trình.

Chia hai vế phương trình cho \({\cos ^2}{x \over 2}\) ta được :

\(\eqalign{& {\tan ^2}{x \over 2} + 2\tan {x \over 2} – 2 = {1 \over 2}\left( {1 + {{\tan }^2}{x \over 2}} \right) \cr & \Leftrightarrow {\tan ^2}{x \over 2} + 4\tan {x \over 2} – 5 = 0 \cr & \Leftrightarrow \left[ {\matrix{{\tan {x \over 2} = 1} \cr {\tan {x \over 2} = – 5} \cr} } \right. \Leftrightarrow \left[ {\matrix{{{x \over 2} = {\pi \over 4} + k\pi } \cr {{x \over 2} = \alpha + k\pi } \cr} } \right.\,\left( {\text{ với }\,\tan \alpha = – 5} \right) \cr & \Leftrightarrow \left[ {\matrix{{x = {\pi \over 2} + k2\pi } \cr {x = 2\alpha + k2\pi } \cr} } \right.\,\left( {k \in\mathbb Z} \right) \cr} \)

 

Câu 48 trang 48 SGK Đại số và Giải tích 11 Nâng cao

 a. Chứng minh rằng  \(\sin {\pi \over {12}} = {{\sqrt 3 – 1} \over {2\sqrt 2 }}\)

b. Giải các phương trình \(2\sin x – 2\cos x =1 – \sqrt 3 \) bằng cách biến đổi vế trái về dạng \(C\sin(x + α)\).

c. Giải phương trình \(2\sin x – 2\cos x =1 – \sqrt 3 \) bằng cách bình phương hai vế.

Giải

a. Ta có:

\(\eqalign{
& \sin {\pi \over {12}} = \sin \left( {{\pi \over 3} – {\pi \over 4}} \right) \cr
& = \sin {\pi \over 3}\cos {\pi \over 4} – \sin {\pi \over 4}\cos {\pi \over 3} \cr
& = {{\sqrt 3 } \over 2}.{{\sqrt 2 } \over 2} – {{\sqrt 2 } \over 2}.{1 \over 2} \cr
& = {{\sqrt 6 – \sqrt 2 } \over 4} = {{\sqrt 2 \left( {\sqrt 3 – 1} \right)} \over 4} \cr
& = {{\sqrt 3 – 1} \over {2\sqrt 2 }} \cr} \) 

b. Ta có:

\(\eqalign{& 2\sin x – 2\cos x = 1 – \sqrt 3 \cr & \Leftrightarrow {1 \over {\sqrt 2 }}\sin x – {1 \over {\sqrt 2 }}\cos x = {{1 – \sqrt 3 } \over {2\sqrt 2 }} \cr & \Leftrightarrow \sin x.\cos {\pi \over 4} – \sin {\pi \over 4}\cos x = – \sin {\pi \over {12}} \cr & \Leftrightarrow \sin \left( {x – {\pi \over 4}} \right) = \sin \left( { – {\pi \over {12}}} \right) \cr & \Leftrightarrow \left[ {\matrix{{x – {\pi \over 4} = – {\pi \over {12}} + k2\pi } \cr
{x – {\pi \over 4} = \pi + {\pi \over {12}} + k2\pi } \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{x = {\pi \over 6} + k2\pi } \cr {x = {{4\pi } \over 3} + k2\pi } \cr} } \right.\left( {k \in\mathbb Z} \right) \cr} \) 

c. Chú ý rằng \(1 – \sqrt 3 < 0\), ta đặt điều kiện \(\sin x – \cos x < 0\) rồi bình phương hai vế của phương trình thì được :

\(\eqalign{& 4\left( {1 – \sin 2x} \right) = 4 – 2\sqrt 3 \cr & \Leftrightarrow \sin 2x = {{\sqrt 3 } \over 2} \Leftrightarrow \left[ {\matrix{{x = {\pi \over 6} + k\pi } \cr {x = {\pi \over 3} + k\pi } \cr}\,\,(k\in\mathbb Z) } \right. \cr} \) 

Thử vào điều kiện \(\sin x – \cos x < 0\), ta thấy :

* Họ nghiệm \(x = {\pi \over 6} + k\pi \) thỏa mãn điều kiện \(\sin x – \cos x < 0\) khi và chỉ khi \(k\) chẵn, tức là \(x = {\pi \over 6} + 2m\pi \) với \(m \in\mathbb Z\).

* Họ nghiệm \(x = {\pi \over 3} + k\pi \) thỏa mãn điều kiện \(\sin x  – \cos x < 0\) khi và chỉ khi \(k\) lẻ, tức là \(x = {\pi \over 3} + \left( {2m + 1} \right)\pi = {{4\pi } \over 3} + 2m\pi \) với \(m \in\mathbb Z\).

Ta có kết quả như đã nêu ở câu b. 

 

Câu 49 trang 48 SGK Đại số và Giải tích 11 Nâng cao

Giải phương trình :

\({{1 + \cos 2x} \over {\cos x}} = {{\sin 2x} \over {1 – \cos 2x}}\) 

Giải

ĐKXĐ :\(\cos x \ne 0\,\text{ và }\,\cos 2x \ne 1.\) Với điều kiện đó, ta có:

\(\eqalign{& {{1 + \cos 2x} \over {\cos x}} = {{\sin 2x} \over {1 – \cos 2x}} \cr & \Leftrightarrow {{2{{\cos }^2}x} \over {\cos x}} = {{2\sin x\cos x} \over {2{{\sin }^2}x}} \cr & \Leftrightarrow 1 – {1 \over {2\sin x}} = 0 \cr & \Leftrightarrow \sin x = {1 \over 2} \Leftrightarrow \left[ {\matrix{{x = {\pi \over 6} + k2\pi \,\left( \text{nhận} \right)} \cr {x = {{5\pi } \over 6} + k2\pi \,\left( \text{nhận} \right)} \cr} } \right. \cr} \)

 

Câu 50 trang 48 SGK Đại số và Giải tích 11 Nâng cao

Cho phương trình  \({{{{\sin }^3}x + {{\cos }^3}x} \over {2\cos x – \sin x}} = \cos 2x.\)

a. Chứng minh rằng \(x = {\pi \over 2} + k\pi \) nghiệm đúng phương trình.

b. Giải phương trình bằng cách đặt \(\tan x = t\) (khi \(x \ne {\pi \over 2} + k\pi \)   )

Giải

a. Thay \(x = {\pi \over 2} + k\pi \) vào phương trình ta được :

\({{{{\left( { – 1} \right)}^{3k}}} \over { – {{\left( { – 1} \right)}^k}}} = \cos \pi \Leftrightarrow – 1 = – 1\) (luôn đúng)

Vậy \(x = {\pi \over 2} + k\pi \) là nghiệm phương trình

b. * \(x = {\pi \over 2} + k\pi \) là nghiệm phương trình.

* Với \(x \ne {\pi \over 2} + k\pi \) chia tử và mẫu của vế trái cho \({\cos ^3}x\) ta được :

\({{{{\tan }^3}x + 1} \over {2\left( {1 + {{\tan }^2}x} \right) – \tan x\left( {1 + {{\tan }^2}x} \right)}} = {{1 – {{\tan }^2}x} \over {1 + {{\tan }^2}x}}\) 

Đặt \(t = \tan x\) ta được :

\(\eqalign{& {{{t^3} + 1} \over {\left( {2 – t} \right)\left( {1 + {t^2}} \right)}} = {{1 – {t^2}} \over {1 + {t^2}}} \cr & \Leftrightarrow {t^3} + 1 = \left( {{t^2} – 1} \right)\left( {t – 2} \right) \cr & \Leftrightarrow {t^3} + 1 = {t^3} – 2{t^2} – t + 2 \cr & \Leftrightarrow 2{t^2} + t – 1 = 0 \Leftrightarrow \left[ {\matrix{
{t = – 1} \cr {t = {1 \over 2}} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{\tan x = – 1} \cr {\tan x = {1 \over 2}} \cr} } \right. \Leftrightarrow \left[ {\matrix{{x = – {\pi \over 4} + k\pi } \cr {x = \alpha + k\pi } \cr} } \right. \cr & \text{ với }\,\tan \alpha = {1 \over 2} \cr} \) 

Vậy phương trình đã cho có nghiệm :\(x = {\pi \over 2} + k\pi ,x = – {\pi \over 4} + k\pi ,x = \alpha + k\pi \,\left( {k \in\mathbb Z} \right)\)

 

Giaibaitap.me

Xem thêm bài viết thuộc chuyên mục: Giáo Dục