Bài tập toán lớp 6: lũy thừa với số mũ tự nhiên và các phép toán

Lũy thừa với số mũ tự nhiên là khái niệm rất cơ bản nhưng hoàn toàn mới với các em học sinh lớp 6. Đây là một trong những kiến thức vô cùng quan trong nên các em cần nắm vững. Trong bài viết này, vuongquocdongu.com sẽ cùng nhau tổng hợp lại các kiến thức về lũy thừa với số mũ tự nhiên và làm bài tập toán lớp 6: lũy thừa với số mũ tự nhiên và các phép toán để giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán được tốt nhất.
| ✅ Lũy thừa là gì? | ⭐ Lũy thừa bậc n của a là tích số của a với chính nó (n lần). Kết quả của phép toán lũy thừa là tích số của phép nhân có n thừa số a nhân với nhau. |
| ✅ Ký hiệu | ⭐ Lũy thừa ký hiệu là an, đọc là lũy thừa bậc n của a, hoặc a mũ n. |
Lý thuyết Lũy thừa với số mũ tự nhiên
1. Lũy thừa với số mũ tự nhiên
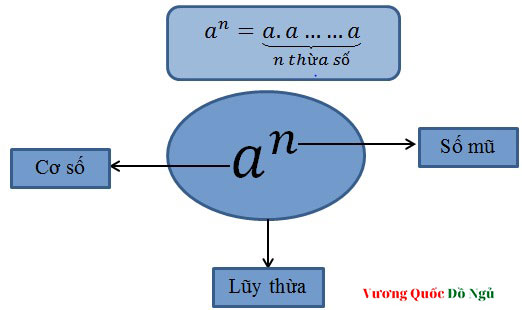
Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a:
an = a.a…..a (n thừa số a) (n khác 0)
a được gọi là cơ số.
n được gọi là số mũ.
2. Nhân hai lũy thừa cùng cơ số
am. an = am+n
Khi nhân hai lũy thừa cùng cơ số, ta giữa nguyên cơ số và cộng các số mũ.
3. Chia hai lũy thừa cùng cơ số
am : an = am-n (a ≠ 0 ; m ≠ 0)
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ cho nhau.
4. Lũy thừa của lũy thừa
(am)n = am.n
Ví dụ: (32)4 = 32.4 = 38
5. Nhân hai lũy thừa cùng số mũ, khác sơ số
am . bm = (a.b)m
ví dụ : 33 . 43 = (3.4)3 = 123
6. Chia hai lũy thừa cùng số mũ, khác cơ số
am : bm = (a : b)m
ví dụ : 84 : 44 = (8 : 4)4 = 24
7. Một vài quy ước
1n = 1 ví dụ : 12017 = 1
a0 = 1 ví dụ : 20170 = 1
Bài tập vận dụng có đáp án
Bài 1: So sánh:
a) 536 và 1124
b) 32n và 23n (n ∈ N*)
c) 523 và 6.522
d) 213 và 216
e) 2115 và 275.498
f) 7245 – 7244 và 7244 – 7243
Giải:
a) 536 = 512 (53)12 = 12512; 1124 = 112.12 = (112)12 = 12112
Mà 12512 > 12112 => 536 > 12112
b) Tương tự
c) Ta có: 523 = 5.522 < 6.522
d) Tương tự.
e) 2115 = (7.3)15 = 715.315
275.498 = (33)5.(72)8 = 315.716 = 7.315.715 > 315.715 = 2115
=> 275.498 > 2115.
f) 7245 – 7244 = 7244.(72 – 1) = 7244.71
7244 – 7243 = 7243.(72 – 1) = 7243.71
Mà 7243.71 < 7244.71 nên suy ra: 7244 – 7243 < 7245 – 7244
Bài 2: Tính giá trị biểu thức (Thu gọn các tổng sau):
a) A = 2 + 22 + 23 + … + 22017
b) B = 1 + 32 + 34 + … + 32018
c) C = – 5 + 52 – 53 + 54 – … – 52017 + 52018
Giải:
a) Ta có: A = 2 + 22 + 23 + … + 22017
2A = 2.( 2 + 22 + 23 + … + 22017)
2A = 22 + 23 + 24 + … + 22018
2A – A = (22 + 23 + 24 + … + 22018) – (2 + 22 + 23 + … + 22017)
A = 22018 – 2
b) B = 1 + 32 + 34 + … + 32018
32.B = 32.( 1 + 32 + 34 + … + 32018)
9B = 32 + 34 + 36 + … + 32020
9B – B = (32 + 34 + 36 + … + 32020) – (1 + 32 + 34 + … + 32018)
8B = 32020 – 1
B = (32020 – 1) : 8.
c) C = – 5 + 52 – 53 + 54 – … – 52017 + 52018
5C = 5.( – 5 + 52 – 53 + 54 – … – 52017 + 52018)
5C = -52 + 53 – 54 + 55 – … – 52018 + 52019
5C + C = (-52 + 53 – 54 + 55 – … – 52018 + 52019) + (- 5 + 52 – 53 + 54 – … – 52017 + 52018)
6C = 52019 – 5
C = (52019 – 5) : 6
Bài 3: Thực hiện các phép tính sau:
a) 37.275.813
b) 1006.10005.100003
c) 365 : 185
d) 24.55 + 52.53
e) 1254 : 58
f) 81.(27 + 915) : (35 + 332)
Giải:
a) 37.275.813 = 37.(33)5.(34)3 = 37.315.312 = 37+15+12 = 334.
b) Tương tự.
c) 365 : 185 = (36 : 18)5 = 25 = 32.
d) 55 + 52.53 = 24.55 + 55 = 55.(24 + 1) = 55.25 = 55.52 = 57.
e) 1254 : 58 = (53)4 : 58 = 512 : 58 = 512-8 = 54 = 625.
f) 81.(27 + 915) : (35 + 332) = 34.(33 + 330) : [35(1 + 327)]
= 34.33.(1 + 327) : [35.(1 + 327)]
= 37 : 35 = 37-5 = 32 = 9.
Hoặc: 81.(27 + 915) : (35 + 332) = 34.(33 + 330) : (35 + 332)
= 32.(33.32 + 330.32) : (35 + 332)
= 32(35 + 332) : (35 + 332)
= 32 = 9
Bài 4: Tìm số tự nhiên x biết rằng
a) 1 + 3 + 5 + … + x = 1600 (x là số tự nhiên lẻ).
Tự giải.
b) 2x + 2x + 3 = 144
Giải:
Ta có: 2x + 2x + 3 = 144
=> 2x + 2x.23 = 144
=> 2x.(1 + 8) = 144
=> 2x.9 = 144
=> 2x = 144 : 9 = 16 = 24
=> x = 4.
c) (x – 5)2016 = (x – 5)2018
=> (x – 5)2018 – (x – 5)2016 = 0
=> (x – 5)2016.[(x – 5)2 – 1] = 0
=> x – 5 = 0 hoặc x – 5 = 1 hoặc x – 5 = -1
=> x = 5 hoặc x = 6 hoặc x = 4 (Thỏa mãn x ∈ N).
Đ/s: x ∈ {4; 5; 6}.
d) (2x + 1)3 = 9.81
Tự trình bày.
Bài 5: Tìm tập hợp các số tự nhiên x, biết rằng lũy thừa 52x – 1 thỏa mãn điều kiện:
100 < 52x – 1 < 56.
Giải:
Ta có: 100 < 52x – 1 < 56
=> 52 < 100 < 52x-1 < 56
=> 2 < 2x – 1 < 6
=> 2 + 1 < 2x < 6 + 1
=> 3 < 2x < 7
Vì x ∈ N nên suy ra: x ∈ {2; 3} là thỏa mãn.
Bài tập về nhà
Bài tập 1: Viết gọn các tích sau dưới dạng lũy thừa.
a) 4 . 4 . 4 . 4 . 4
c) 2 . 4 . 8 . 8 . 8 . 8
b) 10 . 10 . 10 . 100
d) x . x . x . x
Bài tập 2: Tính giá trị của các biểu thức sau.
a) a4.a6
b) (a5)7
c) (a3)4 . a9
d) (23)5.(23)4
Bài toán 3: Viết các tích sau dưới dạng một lũy thừa.
a) 48. 220; 912 . 275 . 814 ; 643 . 45 . 162
b) 2520. 1254; x7 . x4 . x 3 ; 36 . 46
c) 84. 23. 162 ; 23 . 22 . 83 ; y . y7
Bài toán 4: Tính giá trị các lũy thừa sau :
a) 22, 23, 24 , 25 , 26 , 27 , 28 , 29 , 210.
b) 32, 33, 34 , 35.
c) 42, 43, 44.
d) 52, 53, 54.
Bài toán 5: Viết các thương sau dưới dạng một lũy thừa.
a) 49: 44; 178 : 175 ; 210 : 82 ; 1810 : 310 ; 275 : 813
b) 106: 100 ; 59: 253 ; 410 : 643 ; 225 : 324 : 184 : 94
Bài toán 6: Viết các tổng sau thành một bình phương.
a) 13+ 23
b) 13 + 23 + 33
c) 13 + 23 + 33 + 43
Bài toán 7: Tìm x N, biết.
a) 3x. 3 = 243
b) 2x. 162 = 1024
c) 64.4x = 168
d) 2x = 16
Bài toán 8: Thực hiện các phép tính sau bằng cách hợp lý.
a) (217+ 172).(915– 315).(24 – 42)
b) (82017– 82015) : (82104.8)
c) (13+ 23+ 34 + 45).(13 + 23 + 33 + 43).(38 – 812)
d) (28+ 83) : (25.23)
Bài toán 9: Viết các kết quả sau dưới dạng một lũy thừa.
a) 1255: 253
b) 276: 93
c) 420: 215
d) 24n: 22n
e) 644. 165: 420
Bài toán 9: Viết các kết quả sau dưới dạng một lũy thừa.
a) 1255 : 253
b) 276 : 93
c) 420 : 215
d) 24n : 22n
e) 644 . 165 : 420
g) 324 : 86
Bài toán 10 : Tìm x, biết.
a) 2x.4 = 128
b) (2x + 1)3 = 125
c) 2x – 26 = 6
d) 64.4x = 45
e) 27.3x = 243
g) 49.7x = 2401
h) 3x = 81
k) 34.3x = 37
n) 3x + 25 = 26.22 + 2.30
Bài toán 11: So sánh
a) 26 và 82 ; 53 và 35 ; 32 và 23 ; 26 và 62
b) A = 2009.2011 và B = 20102
c) A = 2015.2017 và B = 2016.2016
d) 20170 và 12017
Bài toán 12: Cho A = 1 + 21 + 22 + 23 + … + 22007
a) Tính 2A
b) Chứng minh : A = 22008 – 1
Bài toán 13: Cho A = 1 + 3 + 32 + 33 + 34 + 35 + 36 + 37
a) Tính 3A
b) Chứng minh A = (38 – 1) : 2
Bài toán 14: Cho B = 1 + 3 + 32 + … + 32006
a) Tính 3B
b) Chứng minh: A = (32007 – 1) : 2
Bài toán 15: Cho C = 1 + 4 + 42 + 43 + 45 + 46
a) Tính 4C
b) Chứng minh: A = (47 – 1) : 3
Bài Toàn 16: Tính tổng
a) S = 1 + 2 + 22 + 23 + … + 22017
b) S = 3 + 32 + 33 + ….+ 32017
c) S = 4 + 42 + 43 + … + 42017
d) S = 5 + 52 + 53 + … + 52017
Bài tập Toán lớp 6: Lũy thừa với số mũ tự nhiên và các phép toán tổng hợp toàn bộ kiến thức lý thuyết quan trọng, các dạng bài tập vận dụng và hàng loạt bài tập về nhà cho các em tham khảo.
Nhờ đó, nắm thật chắc kiến thức dạng Toán liên quan đến lũy thừa, số mũ để ngày càng học tốt môn Toán 6. Năm 2021 – 2022, sẽ có 3 bộ sách Toán 6 mới là Chân trời sáng tạo, Kết nối tri thức với cuộc sống và Cánh diều, các em có thể xem trước 3 bộ sách để vào năm học không còn bỡ ngỡ.
Lý thuyết Lũy thừa với số mũ tự nhiên
1. Lũy thừa với số mũ tự nhiên
Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a:
an = a.a…..a (n thừa số a) (n khác 0)
a được gọi là cơ số.
n được gọi là số mũ.
2. Nhân hai lũy thừa cùng cơ số
am. an = am+n
Khi nhân hai lũy thừa cùng cơ số, ta giữa nguyên cơ số và cộng các số mũ.
3. Chia hai lũy thừa cùng cơ số
am : an = am-n (a ≠ 0 ; m ≠ 0)
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ cho nhau.
4. Lũy thừa của lũy thừa
(am)n = am.n
Ví dụ: (32)4 = 32.4 = 38
5. Nhân hai lũy thừa cùng số mũ, khác sơ số
am . bm = (a.b)m
ví dụ : 33 . 43 = (3.4)3 = 123
6. Chia hai lũy thừa cùng số mũ, khác cơ số
am : bm = (a : b)m
ví dụ : 84 : 44 = (8 : 4)4 = 24
7. Một vài quy ước
1n = 1 ví dụ : 12017 = 1
a0 = 1 ví dụ : 20170 = 1
Bài tập vận dụng có đáp án
Bài 1: So sánh:
a) 536 và 1124
b) 32n và 23n (n ∈ N*)
c) 523 và 6.522
d) 213 và 216
e) 2115 và 275.498
f) 7245 – 7244 và 7244 – 7243
Giải:
a) 536 = 512 (53)12 = 12512; 1124 = 112.12 = (112)12 = 12112
Mà 12512 > 12112 => 536 > 12112
b) Tương tự
c) Ta có: 523 = 5.522 < 6.522
d) Tương tự.
e) 2115 = (7.3)15 = 715.315
275.498 = (33)5.(72)8 = 315.716 = 7.315.715 > 315.715 = 2115
=> 275.498 > 2115.
f) 7245 – 7244 = 7244.(72 – 1) = 7244.71
7244 – 7243 = 7243.(72 – 1) = 7243.71
Mà 7243.71 < 7244.71 nên suy ra: 7244 – 7243 < 7245 – 7244
Bài 2: Tính giá trị biểu thức (Thu gọn các tổng sau):
a) A = 2 + 22 + 23 + … + 22017
b) B = 1 + 32 + 34 + … + 32018
c) C = – 5 + 52 – 53 + 54 – … – 52017 + 52018
Giải:
a) Ta có: A = 2 + 22 + 23 + … + 22017
2A = 2.( 2 + 22 + 23 + … + 22017)
2A = 22 + 23 + 24 + … + 22018
2A – A = (22 + 23 + 24 + … + 22018) – (2 + 22 + 23 + … + 22017)
A = 22018 – 2
b) B = 1 + 32 + 34 + … + 32018
32.B = 32.( 1 + 32 + 34 + … + 32018)
9B = 32 + 34 + 36 + … + 32020
9B – B = (32 + 34 + 36 + … + 32020) – (1 + 32 + 34 + … + 32018)
8B = 32020 – 1
B = (32020 – 1) : 8.
c) C = – 5 + 52 – 53 + 54 – … – 52017 + 52018
5C = 5.( – 5 + 52 – 53 + 54 – … – 52017 + 52018)
5C = -52 + 53 – 54 + 55 – … – 52018 + 52019
5C + C = (-52 + 53 – 54 + 55 – … – 52018 + 52019) + (- 5 + 52 – 53 + 54 – … – 52017 + 52018)
6C = 52019 – 5
C = (52019 – 5) : 6
Bài 3: Thực hiện các phép tính sau:
a) 37.275.813
b) 1006.10005.100003
c) 365 : 185
d) 24.55 + 52.53
e) 1254 : 58
f) 81.(27 + 915) : (35 + 332)
Giải:
a) 37.275.813 = 37.(33)5.(34)3 = 37.315.312 = 37+15+12 = 334.
b) Tương tự.
c) 365 : 185 = (36 : 18)5 = 25 = 32.
d) 55 + 52.53 = 24.55 + 55 = 55.(24 + 1) = 55.25 = 55.52 = 57.
e) 1254 : 58 = (53)4 : 58 = 512 : 58 = 512-8 = 54 = 625.
f) 81.(27 + 915) : (35 + 332) = 34.(33 + 330) : [35(1 + 327)]
= 34.33.(1 + 327) : [35.(1 + 327)]
= 37 : 35 = 37-5 = 32 = 9.
Hoặc: 81.(27 + 915) : (35 + 332) = 34.(33 + 330) : (35 + 332)
= 32.(33.32 + 330.32) : (35 + 332)
= 32(35 + 332) : (35 + 332)
= 32 = 9
Bài 4: Tìm số tự nhiên x biết rằng
a) 1 + 3 + 5 + … + x = 1600 (x là số tự nhiên lẻ).
Tự giải.
b) 2x + 2x + 3 = 144
Giải:
Ta có: 2x + 2x + 3 = 144
=> 2x + 2x.23 = 144
=> 2x.(1 + 8) = 144
=> 2x.9 = 144
=> 2x = 144 : 9 = 16 = 24
=> x = 4.
c) (x – 5)2016 = (x – 5)2018
=> (x – 5)2018 – (x – 5)2016 = 0
=> (x – 5)2016.[(x – 5)2 – 1] = 0
=> x – 5 = 0 hoặc x – 5 = 1 hoặc x – 5 = -1
=> x = 5 hoặc x = 6 hoặc x = 4 (Thỏa mãn x ∈ N).
Đ/s: x ∈ {4; 5; 6}.
d) (2x + 1)3 = 9.81
Tự trình bày.
Bài 5: Tìm tập hợp các số tự nhiên x, biết rằng lũy thừa 52x – 1 thỏa mãn điều kiện:
100 < 52x – 1 < 56.
Giải:
Ta có: 100 < 52x – 1 < 56
=> 52 < 100 < 52x-1 < 56
=> 2 < 2x – 1 < 6
=> 2 + 1 < 2x < 6 + 1
=> 3 < 2x < 7
Vì x ∈ N nên suy ra: x ∈ {2; 3} là thỏa mãn.
Bài tập về nhà
Bài tập 1: Viết gọn các tích sau dưới dạng lũy thừa.
a) 4 . 4 . 4 . 4 . 4
c) 2 . 4 . 8 . 8 . 8 . 8
b) 10 . 10 . 10 . 100
d) x . x . x . x
Bài tập 2: Tính giá trị của các biểu thức sau.
a) a4.a6
b) (a5)7
c) (a3)4 . a9
d) (23)5.(23)4
Bài toán 3: Viết các tích sau dưới dạng một lũy thừa.
a) 48. 220; 912 . 275 . 814 ; 643 . 45 . 162
b) 2520. 1254; x7 . x4 . x 3 ; 36 . 46
c) 84. 23. 162 ; 23 . 22 . 83 ; y . y7
Bài toán 4: Tính giá trị các lũy thừa sau :
a) 22, 23, 24 , 25 , 26 , 27 , 28 , 29 , 210.
b) 32, 33, 34 , 35.
c) 42, 43, 44.
d) 52, 53, 54.
Bài toán 5: Viết các thương sau dưới dạng một lũy thừa.
a) 49: 44; 178 : 175 ; 210 : 82 ; 1810 : 310 ; 275 : 813
b) 106: 100 ; 59: 253 ; 410 : 643 ; 225 : 324 : 184 : 94
Bài toán 6: Viết các tổng sau thành một bình phương.
a) 13+ 23
b) 13 + 23 + 33
c) 13 + 23 + 33 + 43
Bài toán 7: Tìm x N, biết.
a) 3x. 3 = 243
b) 2x. 162 = 1024
c) 64.4x = 168
d) 2x = 16
Bài toán 8: Thực hiện các phép tính sau bằng cách hợp lý.
a) (217+ 172).(915– 315).(24 – 42)
b) (82017– 82015) : (82104.8)
c) (13+ 23+ 34 + 45).(13 + 23 + 33 + 43).(38 – 812)
d) (28+ 83) : (25.23)
Bài toán 9: Viết các kết quả sau dưới dạng một lũy thừa.
a) 1255: 253
b) 276: 93
c) 420: 215
d) 24n: 22n
e) 644. 165: 420
Bài toán 9: Viết các kết quả sau dưới dạng một lũy thừa.
a) 1255 : 253
b) 276 : 93
c) 420 : 215
d) 24n : 22n
e) 644 . 165 : 420
g) 324 : 86
Bài toán 10 : Tìm x, biết.
a) 2x.4 = 128
b) (2x + 1)3 = 125
c) 2x – 26 = 6
d) 64.4x = 45
e) 27.3x = 243
g) 49.7x = 2401
h) 3x = 81
k) 34.3x = 37
n) 3x + 25 = 26.22 + 2.30
Bài toán 11: So sánh
a) 26 và 82 ; 53 và 35 ; 32 và 23 ; 26 và 62
b) A = 2009.2011 và B = 20102
c) A = 2015.2017 và B = 2016.2016
d) 20170 và 12017
Bài toán 12: Cho A = 1 + 21 + 22 + 23 + … + 22007
a) Tính 2A
b) Chứng minh : A = 22008 – 1
Bài toán 13: Cho A = 1 + 3 + 32 + 33 + 34 + 35 + 36 + 37
a) Tính 3A
b) Chứng minh A = (38 – 1) : 2
Bài toán 14: Cho B = 1 + 3 + 32 + … + 32006
a) Tính 3B
b) Chứng minh: A = (32007 – 1) : 2
Bài toán 15: Cho C = 1 + 4 + 42 + 43 + 45 + 46
a) Tính 4C
b) Chứng minh: A = (47 – 1) : 3
Bài Toàn 16: Tính tổng
a) S = 1 + 2 + 22 + 23 + … + 22017
b) S = 3 + 32 + 33 + ….+ 32017
c) S = 4 + 42 + 43 + … + 42017
d) S = 5 + 52 + 53 + … + 52017
Lũy thừa với số mũ tự nhiên – Bài 6 – Toán học 6 – Kết nối tri thức – Cô Vương Hạnh (DỄ HIỂU NHẤT)