✓ chuyên đề trục căn thức ở mẫu của biểu thức: lý thuyết và bài tập

Chuyên đề trục căn thức ở mẫu của biểu thức được xem là dạng toán căn bản trong chương trình Toán 9 và các đề thi tuyển sinh vào lớp 10. Tài liệu dưới dây do vuongquocdongu.com tổng hợp và chia sẻ để giúp các em nắm chắc hơn phần kiến thức về căn thức bậc hai cũng như bài toán rút gọn biểu thức. Qua đó giúp các em có thể ôn tập và rèn luyện tốt cho kì thi tuyển sinh vào lớp 10 sắp tới. Mời các bạn cùng khảo chi tiết nội dung dưới đây nhé!

Cách biến đổi căn bậc hai một cách đơn giản

Dưới đây là những kiến ​​thức cần nhớ về cách thực hiện một phép biến hình đơn giản căn bậc hai:

Trục bán kính ở mẫu số của biểu thức

Đây là lý thuyết và làm thế nào để làm mẫu số của một phân số:

Với các biểu thức (A, B (B> 0) ), chúng ta có;

(A, B (B> 0) )

Với các biểu thức (A, B, C ) ((A geq 0, A neq B ^ {2}) )

Chúng ta có:

( frac {C} { sqrt {A} + B} = frac {C ( sqrt {A} -B)} {AB ^ {2}} )

( frac {C} { sqrt {A} -B} = frac {C ( sqrt {A} + B)} {AB ^ {2}} )

Với các biểu thức (A, B, C ) ((A geq 0, B geq 0, A neq B) )

Chúng ta có:

( frac {C} { sqrt {A} + sqrt {B}} = frac {C ( sqrt {A} – sqrt {B})} {AB} )

( frac {C} { sqrt {A} – sqrt {B}} = frac {C ( sqrt {A} + sqrt {B})} {AB} )

Bài tập về trục căn trong văn mẫu lớp 9

Bài 50 (trang 30 SGK Toán 9 Tập 1): Trục mẫu với giả thiết mọi biểu thức từ đều có nghĩa.

( frac {5} { sqrt {10}} = frac {5 sqrt {10}} { sqrt {10}. sqrt {10}} = frac {5 sqrt {10}} { 10} = frac { sqrt {10}} {2} )

( frac {1} {3 sqrt {20}} = frac {1} {3 sqrt {2 ^ {2} .5}} = frac {1} {3.2 sqrt {5}} = frac {1 sqrt {5}} {6 sqrt {5}. sqrt {5}} = frac { sqrt {5}} {6.5} = frac { sqrt {5}} {30} )

( frac {2 sqrt {2} +2} {5 sqrt {2}} = frac {(2 sqrt {2} +2) sqrt {2}} {5 sqrt {2}. sqrt {2}} = frac {2 ( sqrt {2}) ^ {2} +2 sqrt {2}} {5.2} = frac {4 + 2 sqrt {2}} {10} = frac {2+ sqrt {2}} {5} )

Bài 52 trang 30 SGK toán tập 1, trục căn mẫu, giả sử mọi biểu thức chữ đều có nghĩa.

( frac {1} { sqrt {x} – sqrt {y}}; frac {2ab} { sqrt {a} – sqrt {b}} )

• ( frac {1} { sqrt {x} – sqrt {y}} = frac {1 ( sqrt {x} + sqrt {y})} {( sqrt {x} – sqrt { y}) ( sqrt {x} + sqrt {y})} = frac {( sqrt {x} + sqrt {y})} {xy} )

(Vì (x neq y ) nên ( sqrt {x} neq sqrt {y} )

• ( frac {2ab} { sqrt {a} – sqrt {b}} = frac {2ab ( sqrt {a} + sqrt {b})} {( sqrt {a} – sqrt { b}) ( sqrt {a} + sqrt {b})} = frac {2ab ( sqrt {a} + sqrt {b})} {ab} )

(Vì (a neq b ) nên ( sqrt {a} neq sqrt {b} ).

Các vấn đề trục gốc trong các mẫu khó

Ví dụ 1: Trục căn mẫu của các biểu thức sau

1. ( frac { sqrt {5} – sqrt {3}} { sqrt {2}} )
2. ( frac {26} {5-2 sqrt {3}} )

Ví dụ 2: Trục bán kính mẫu

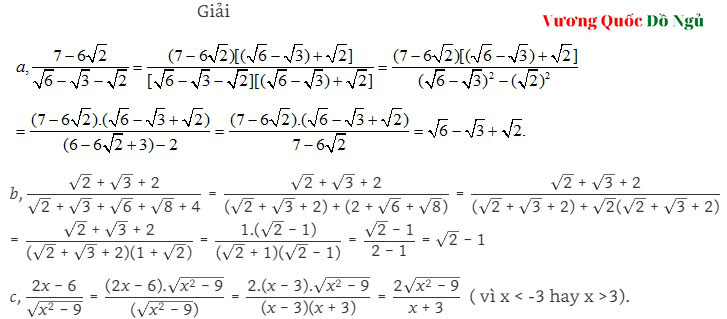
Lý thuyết về trục căn ở mẫu số 3

Công thức nấu ăn:

( frac {M} { sqrt[3]{a} pm sqrt[3]{b}} = frac {M ( sqrt[3]{a ^ {2}} pm sqrt[3]{ab} + sqrt[3]{b ^ {2}})} {( sqrt[3]{a} pm sqrt[3]{b}) ( sqrt[3]{a ^ {2}} pm sqrt[3]{ab} + sqrt[3]{b ^ {2}})} = frac {M ( sqrt[3]{a ^ {2}} pm sqrt[3]{ab} + sqrt[3]{b ^ {2}})} {a pm b} )

Ví dụ: Trục bán kính mẫu: ( frac {1} { sqrt[3]{9} – sqrt[3]{6} + sqrt[3]{4}})

Chúng tôi có: ( frac {1} { sqrt[3]{9} – sqrt[3]{6} + sqrt[3]{4}} = frac { sqrt[3]{3} + sqrt[3]{2}} {( sqrt[3]{2} + sqrt[3]{3}) ( sqrt[3]{9} – sqrt[3]{6} + sqrt[3]{4})} = frac { sqrt[3]{2} + sqrt[3]{3}} {( sqrt[3]{2}) ^ {3} + ( sqrt[3]{3}) ^ {3})} = frac { sqrt[3]{2} + sqrt[3]{3}} {5} )

Xem nội dung chi tiết bài giảng dưới đây:

(Nguồn: www.youtube.com)

Xem thêm >>> Cách xác định tâm đường tròn ngoại tiếp tam giác – Toán lớp 9 |